【题目】已知正项数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() 和
和![]() 满足:
满足:![]()
![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)设![]() ,求
,求![]() 的前
的前![]() 项和
项和![]() ;
;
(3)在(2)的条件下,对任意![]() ,
,![]() 都成立,求整数
都成立,求整数![]() 的最大值.
的最大值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)整数
;(3)整数![]() 的最大值为7.
的最大值为7.
【解析】
(1)由4Sn=(an+1)2,知4Sn-1=(an-1+1)2(n≥2),由此得到(an+an-1)(an-an-1-2)=0.从而能求出{an}的通项公式.
(2)由(1)知![]()
,由此利用裂项求和法能求出Tn.
(3)由(2)知![]()
从而得到![]() .由此能求出任意n∈N*,Tn
.由此能求出任意n∈N*,Tn![]() 都成立的整数m的最大值.
都成立的整数m的最大值.
:(1)∵4Sn=(an+1)2,①
∴4Sn-1=(an-1+1)2(n≥2),②
①-②得
4(Sn-Sn-1)=(an+1)2-(an-1+1)2.
∴4an=(an+1)2-(an-1+1)2.
化简得(an+an-1)(an-an-1-2)=0.
∵an>0,∴an-an-1=2(n≥2).
∴{an}是以1为首项,2为公差的等差数列.
∴an=1+(n-1)2=2n-1.
(2)![]() .
.
∴![]() .
.
(3)由(2)知![]()
∴数列{Tn}是递增数列.
∴![]() .
.
∴![]()
∴整数m的最大值是7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
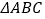 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 成等差数列
成等差数列(1)若
 ,求
,求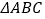 的面积
的面积(2)若
 成等比数列,试判断
成等比数列,试判断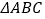 的形状
的形状 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的角
的角 所对的边份别为
所对的边份别为 ,且
,且
(1)求角
 的大小;
的大小;(2)若
 ,求
,求 的周长
的周长 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形
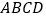 的边长为2,点
的边长为2,点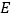 为
为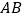 的中点.以
的中点.以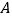 为圆心,
为圆心, 为半径,作弧交
为半径,作弧交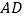 于点
于点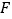 .若
.若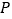 为劣弧
为劣弧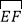 上的动点,则
上的动点,则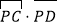 的最小值为__________.
的最小值为__________.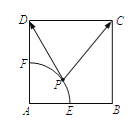
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论中:
①定义在R上的函数f(x)在区间(-∞,0]上是增函数,在区间[0,+∞)上也是增函数,则函数f(x)在R上是增函数;②若f(2)=f(-2),则函数f(x)不是奇函数;③函数y=x-0.5是(0,1)上的减函数;④对应法则和值域相同的函数的定义域也相同;⑤若x0是二次函数y=f(x)的零点,且m<x0<n,那么f(m)f(n)<0一定成立.
写出上述所有正确结论的序号:_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是
A. 先把高三年级的2000名学生编号:1到2000,再从编号为1到50的50名学生中随机抽取1名学生,其编号为
 ,然后抽取编号为
,然后抽取编号为 的学生,这样的抽样方法是分层抽样法
的学生,这样的抽样方法是分层抽样法B. 线性回归直线
 不一定过样本中心点
不一定过样本中心点
C. 若两个随机变量的线性相关性越强,则相关系数
 的值越接近于1
的值越接近于1D. 若一组数据1、
 、3的平均数是2,则该组数据的方差是
、3的平均数是2,则该组数据的方差是
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)的二次项系数为a(a<0).1,3是函数y=f(x)+2x的两个零点.若方程f(x)+6a=0有两个相等的根,求f(x)的解析式.
相关试题

