【题目】在直角坐标系![]() 中,点
中,点![]() 到两点
到两点![]() 的距离之和等于4,设点
的距离之和等于4,设点![]() 的轨迹为
的轨迹为![]()
(1)求曲线![]() 的方程;
的方程;
(2)设![]() 、
、![]() 、
、![]() 是曲线
是曲线![]() 上的三点.若
上的三点.若![]() ,求线段
,求线段![]() 的中点
的中点![]() 的轨迹方程.
的轨迹方程.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
试题分析:(1)由椭圆定义可知,点![]() 的轨迹
的轨迹![]() 是以
是以![]() 为焦点,长半轴长为
为焦点,长半轴长为![]() 的椭圆,即可求出椭圆的方程;(2)设
的椭圆,即可求出椭圆的方程;(2)设![]() ,则
,则 ![]() .由
.由![]() ,得
,得 ![]() .因为M是椭圆C上一点,所以
.因为M是椭圆C上一点,所以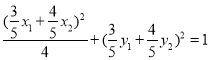 ,
,
即![]() ,得
,得
![]() ,故
,故 ![]() .又线段AB的中点的坐标为
.又线段AB的中点的坐标为![]() ,所以
,所以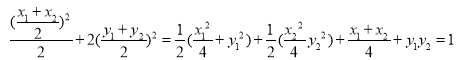 ,
,
从而线段AB的中点![]() 在椭圆
在椭圆![]() 上.
上.
试题解析:解:(1)由椭圆定义可知,
点![]() 的轨迹
的轨迹![]() 是以
是以![]() 为焦点,长半轴长为
为焦点,长半轴长为![]() 的椭圆.…(3分)
的椭圆.…(3分)
故曲线![]() 的方程为
的方程为![]()
(2)设![]() ,则
,则 ![]() .
.
由![]() ,得
,得 ![]() .
.
因为M是椭圆C上一点,所以
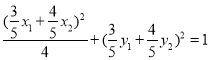 ,
,
即![]() ,
,
得 ![]() ,故
,故 ![]() .
.
又线段AB的中点的坐标为![]() ,
,
所以 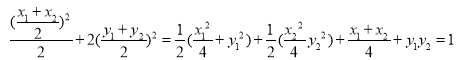 ,
,
从而线段AB的中点![]() 在椭圆
在椭圆![]() 上.
上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业.根据规划,本年度投入
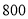 万元,以后每年投入将比上年减少
万元,以后每年投入将比上年减少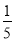 .本年度当地旅游业收入估计为
.本年度当地旅游业收入估计为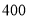 万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加
万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加 .
.(Ⅰ)设
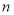 年内(本年度为第一年)总投入为
年内(本年度为第一年)总投入为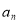 万元,旅游业总收入为
万元,旅游业总收入为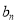 万元.写出
万元.写出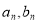 的表达式;
的表达式;(Ⅱ)至少经过几年旅游业的总收入才能超过总投入?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
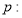 实数
实数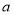 满足不等式
满足不等式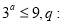 函数
函数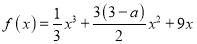 无极值点.
无极值点.(1)若“
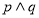 ”为假命题,“
”为假命题,“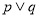 ”为真命题,求实数
”为真命题,求实数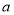 的取值范围;
的取值范围;(2)已知“
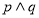 ”为真命题,并记为
”为真命题,并记为 ,且
,且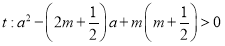 ,若
,若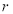 是
是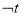 的必要不充分条件,求正整数
的必要不充分条件,求正整数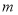 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
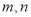 是不同的直线,
是不同的直线,  是不同的平面,已知
是不同的平面,已知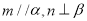 ,下列说法正确的是 ( )
,下列说法正确的是 ( )A. 若
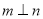 ,则
,则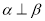 B. 若
B. 若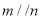 ,则
,则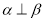
C. 若
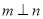 ,则
,则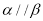 D. 若
D. 若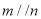 ,则
,则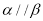
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:
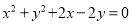 的圆心为C,
的圆心为C, 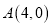 ,
, 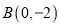
(Ⅰ)在
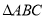 中,求
中,求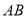 边上的高CD所在的直线方程;
边上的高CD所在的直线方程;(Ⅱ)求与圆C相切且在两坐标轴上的截距相等的直线方程
-
科目: 来源: 题型:
查看答案和解析>>【题目】某届奥运会上,中国队以26金18银26铜的成绩称金牌榜第三、奖牌榜第二,某校体育爱好者在高三 年级一班至六班进行了“本届奥运会中国队表现”的满意度调查(结果只有“满意”和“不满意”两种),从被调查的学生中随机抽取了50人,具体的调查结果如下表:

(1)在高三年级全体学生中随机抽取一名学生,由以上统计数据估计该生持满意态度的概率;
(2)若从一班至二班的调查对象中随机选取4人进行追踪调查,记选中的4人中对“本届奥运会中国队表现”不满意的人数为
 ,求随机变量
,求随机变量 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆M过两点A(1,﹣1),B(﹣1,1),且圆心M在直线x+y﹣2=0上.
(1)求圆M的方程.
(2)设P是直线3x+4y+8=0上的动点,PC、PD是圆M的两条切线,C、D为切点,求四边形PCMD面积的最小值.
相关试题

