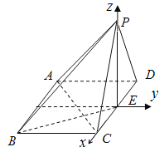
【题目】在四棱柱![]() 中,底面
中,底面![]() 为矩形,面
为矩形,面![]() ⊥平面
⊥平面![]() ,
,![]() =
=![]() =
=![]() =
=![]() ,
,![]() =2,
=2,![]() 是
是![]() 的中点.
的中点.
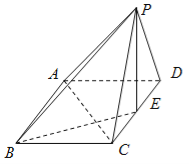
(Ⅰ)求证:![]() ⊥
⊥![]() ;
;
(Ⅱ)求BD与平面![]() 所成角的正弦值.
所成角的正弦值.
参考答案:
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】(Ⅰ)∵PD=PC,E为CD的中点,∴PE⊥CD,
∵平面PCD⊥平面ABCD,∴PE⊥平面ABCD,
∴PE⊥AC,(2分)
在Rt△BCE和Rt△ABC中,![]() ,∠ABC=∠BCE=90°,
,∠ABC=∠BCE=90°,
∴Rt△BCE∽Rt△ABC,(4分)
∴∠BAC=∠CBE,∠ACB=∠BEC,
∴∠EBC+∠ACB=∠CAB+∠ACB=90°,
∴BE⊥CA,(5分)
∵BE∩PE=E,
∴AC⊥平面PBE,
∴AC⊥PB;(6分)
(Ⅱ)以E为坐标原点,如图建立空间直角坐标系,则P(0,0,1),C(1,0,0),![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,(8分)
,(8分)
设平面![]() 的法向量为
的法向量为![]() ,则
,则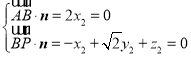 ,取
,取![]() =
=![]() ,则
,则![]() =0,
=0,![]() =-2,∴
=-2,∴![]() =(0,
=(0,![]() ,-2),(10分)
,-2),(10分)
设BD与平面![]() 所成角为
所成角为![]() ,
,
则![]() =
=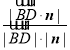 =
=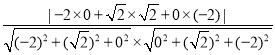 =
=![]() ,(11分)
,(11分)
∴BD与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .(12分)
.(12分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某食品厂定期购买面粉.已知该厂每天需用面粉6t,每吨面粉的价格为1800元,面粉的保管等其他费用为平均每吨每天3元,购面粉每次需支付运费900元.
(1)求该厂多少天购买一次面粉,才能使平均每天所支付的总费用最少?
(2)若提供面粉的公司规定:当一次购买面粉不少于210t时,其价格可享受9折优惠(即原价的90%),问该厂是否考虑利用此优惠条件?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为
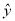 =0.85x-85.71,则下列结论中不正确的是( )
=0.85x-85.71,则下列结论中不正确的是( )A. y与x具有正的线性相关关系
B. 若给变量x一个值,由回归直线方程
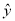 =0.85x-85.71得到一个
=0.85x-85.71得到一个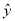 ,则
,则 为该统计量中的估计值
为该统计量中的估计值C. 若该大学某女生身高增加1 cm,则其体重约增加0.85 kg
D. 若该大学某女生身高为170 cm,则可断定其体重必为58.79 kg
-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两名同学在5次数学考试中的成绩统计如下面的茎叶图所示,若A,B两人的平均成绩分别是xA , xB , 观察茎叶图,下列结论正确的是( )
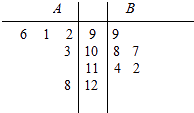
A.xA<xB , B比A成绩稳定
B.xA>xB , B比A成绩稳定
C.xA<xB , A比B成绩稳定
D.xA>xB , A比B成绩稳定 -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)下图是某市今年1月份前30天空气质量指数(AQI)的趋势图.

(1)根据该图数据在答题卷中完成频率分布表,并在图中补全这些数据的频率分布直方图;
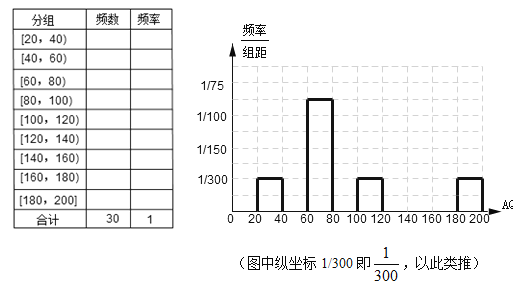
(2)当空气质量指数(AQI)小于100时,表示空气质量优良.某人随机选择当月(按30天计)某一天
到达该市,根据以上信息,能否认为此人到达当天空气质量优良的可能性超过60%?
-
科目: 来源: 题型:
查看答案和解析>>【题目】200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,则时速在[50,70)的汽车大约( )
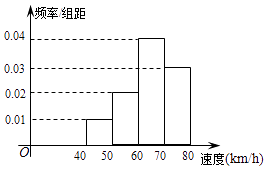
A.60辆
B.80辆
C.100辆
D.120辆 -
科目: 来源: 题型:
查看答案和解析>>【题目】天气预报说,在今后的三天中,每一天下雨的概率均为50%.现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用0,1,2,3,4表示下雨,用5,6,7,8,9表示不下雨;再以每三个随机数作为一组,代表这三天的下雨情况.经随机模拟试验产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,这三天中恰有两天下雨的概率近似为( )
A. 0.30 B. 0.35 C. 0.40 D. 0.50
相关试题

