【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是( )
=0.85x-85.71,则下列结论中不正确的是( )
A. y与x具有正的线性相关关系
B. 若给变量x一个值,由回归直线方程![]() =0.85x-85.71得到一个
=0.85x-85.71得到一个![]() ,则
,则![]() 为该统计量中的估计值
为该统计量中的估计值
C. 若该大学某女生身高增加1 cm,则其体重约增加0.85 kg
D. 若该大学某女生身高为170 cm,则可断定其体重必为58.79 kg
参考答案:
【答案】D
【解析】试题分析:由已知回归方程为![]() =0.85x-85.71,可知0.85>0,y与x具有正的线性相关关系,回归直线方程过(
=0.85x-85.71,可知0.85>0,y与x具有正的线性相关关系,回归直线方程过(![]() ,
, ![]() ),若该大学某女生身高为170 cm,则可推断其体重约为58.79kg,都正确;D错误;若该大学某女生身高增加1cm,则可推断其体重增加0.85kg,应为则其体重约增加0.85kg;
),若该大学某女生身高为170 cm,则可推断其体重约为58.79kg,都正确;D错误;若该大学某女生身高增加1cm,则可推断其体重增加0.85kg,应为则其体重约增加0.85kg;
-
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}满足a1=1,nan+1=(n+1)an+n(n+1),n∈N* . (Ⅰ)证明:数列{
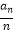 }是等差数列;
}是等差数列;
(Ⅱ)设bn=3n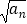 ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速
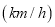 分成六段:
分成六段: 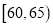 ,
, 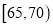 ,
, 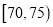 ,
, 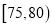 ,
, 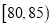 ,
, 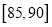 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.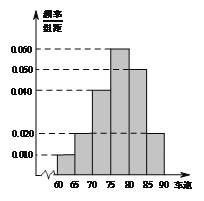
(I)某调查公司在采样中,用到的是什么抽样方法?
(II)求这40辆小型车辆车速的众数、中位数及平均数的估计值;
(III)若从车速在
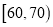 的车辆中任抽取2辆,求车速在
的车辆中任抽取2辆,求车速在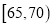 的车辆至少有一辆的概率.
的车辆至少有一辆的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某食品厂定期购买面粉.已知该厂每天需用面粉6t,每吨面粉的价格为1800元,面粉的保管等其他费用为平均每吨每天3元,购面粉每次需支付运费900元.
(1)求该厂多少天购买一次面粉,才能使平均每天所支付的总费用最少?
(2)若提供面粉的公司规定:当一次购买面粉不少于210t时,其价格可享受9折优惠(即原价的90%),问该厂是否考虑利用此优惠条件?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两名同学在5次数学考试中的成绩统计如下面的茎叶图所示,若A,B两人的平均成绩分别是xA , xB , 观察茎叶图,下列结论正确的是( )
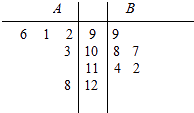
A.xA<xB , B比A成绩稳定
B.xA>xB , B比A成绩稳定
C.xA<xB , A比B成绩稳定
D.xA>xB , A比B成绩稳定 -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱柱
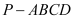 中,底面
中,底面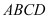 为矩形,面
为矩形,面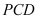 ⊥平面
⊥平面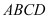 ,
,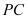 =
=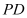 =
=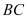 =
= ,
,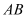 =2,
=2,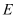 是
是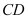 的中点.
的中点.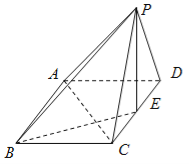
(Ⅰ)求证:
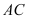 ⊥
⊥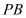 ;
;(Ⅱ)求BD与平面
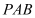 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)下图是某市今年1月份前30天空气质量指数(AQI)的趋势图.

(1)根据该图数据在答题卷中完成频率分布表,并在图中补全这些数据的频率分布直方图;
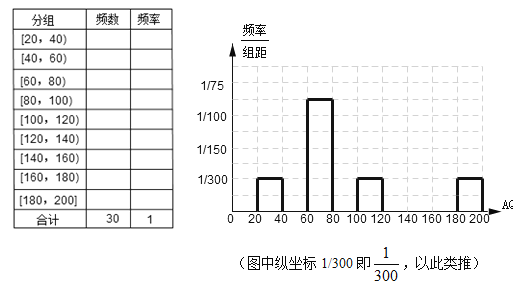
(2)当空气质量指数(AQI)小于100时,表示空气质量优良.某人随机选择当月(按30天计)某一天
到达该市,根据以上信息,能否认为此人到达当天空气质量优良的可能性超过60%?
相关试题

