【题目】记函数 ![]() 的定义域为A,g(x)=lg[(x﹣a﹣1)(2a﹣x)](a<1)的定义域为B,求
的定义域为A,g(x)=lg[(x﹣a﹣1)(2a﹣x)](a<1)的定义域为B,求
(1)A,B;
(2)若BA,求实数a的取值范围.
参考答案:
【答案】
(1)解: ![]() ≥0,等价于
≥0,等价于 ![]() 即x<﹣1或x≥1
即x<﹣1或x≥1
∴A=(﹣∞,﹣1)∪[1,+∞)
由(x﹣a﹣1)(2a﹣x)>0,得(x﹣a﹣1)(x﹣2a)<0.
∵a<1,∴a+1>2a,∴B=(2a,a+1)
(2)解:∵BA,∴2a≥1或a+1≤﹣1,即a≥ ![]() 或a≤﹣2,而a<1,
或a≤﹣2,而a<1,
∴ ![]() ≤a<1或a≤﹣2,
≤a<1或a≤﹣2,
故当BA时,实数a的取值范围是(﹣∞,﹣2]∪[ ![]() ,1)
,1)
【解析】(1)使函数有意义,列出不等式,求出函数的定义域,即可得到集合A,B.(2)结合(1)求出集合A,B,利用BA,建立关于a的不等关系求实数a的取值范围.
【考点精析】利用函数的定义域及其求法对题目进行判断即可得到答案,需要熟知求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知c>0,命题p:函数
 在R上单调递减,命题q:不等式
在R上单调递减,命题q:不等式 的解集是R,若
的解集是R,若 为真命题,
为真命题,  为假命题,求c的取值范围。
为假命题,求c的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
以坐标原点
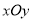 为极点,以
为极点,以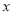 轴正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线
轴正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线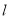 的参数方程为
的参数方程为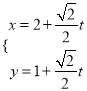 (
(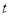 为参数),圆
为参数),圆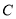 的极坐标方程为
的极坐标方程为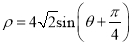 .
.(1)求直线
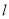 的普通方程与圆
的普通方程与圆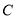 的直角坐标方程;
的直角坐标方程;(2)设圆
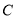 与直线
与直线 交于
交于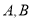 两点,若点
两点,若点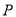 的直角坐标为
的直角坐标为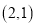 ,求
,求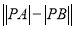 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是定义在R上不恒为0的函数,且对于任意的实数a,b满足f(2)=2,f(ab)=af(b)+bf(a),an=
 (n∈N*),bn=
(n∈N*),bn=  (n∈N*),给出下列命题:
(n∈N*),给出下列命题:
①f(0)=f(1);
②f(x)为奇函数;
③数列{an}为等差数列;
④数列{bn}为等比数列.
其中正确的命题是 . (写出所有正确命题的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,曲线C1的参数方程为
 (t为参数),以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=﹣
(t为参数),以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=﹣ 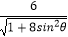 .
.
(1)求曲线C1的普通方程与曲线C2的直角坐标方程;
(2)若C1上的点P对应的参数为t= ,Q为C2上的动点,求PQ中点M到直线C3:
,Q为C2上的动点,求PQ中点M到直线C3: 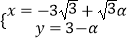 (α为参数)距离的最小值.
(α为参数)距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:2x≤256且log2x≥
 ,
,
(1)求x的取值范围;
(2)求函数log2( )log2(
)log2(  )的最大值和最小值以及相应的x的取值.
)的最大值和最小值以及相应的x的取值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=ax2+2x+c(a≠0),函数f(x)对于任意的都满足条件f(1+x)=f(1﹣x).
(1)若函数f(x)的图象与y轴交于点(0,2),求函数f(x)的解析式;
(2)若函数f(x)在区间(0,1)上有零点,求实数c的取值范围.
相关试题

