【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (t为参数),以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=﹣
(t为参数),以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=﹣ ![]() .
.
(1)求曲线C1的普通方程与曲线C2的直角坐标方程;
(2)若C1上的点P对应的参数为t= ![]() ,Q为C2上的动点,求PQ中点M到直线C3:
,Q为C2上的动点,求PQ中点M到直线C3: ![]() (α为参数)距离的最小值.
(α为参数)距离的最小值.
参考答案:
【答案】
(1)解:∵曲线C1的参数方程为 ![]() (t为参数),
(t为参数),
∴ ![]() ,
,
∴曲线C1的普通方程为(x+4)2+(y﹣3)2=1.
∵曲线C2的极坐标方程为ρ=﹣ ![]() ,
,
∴ρ2+8ρ2sin2θ=36,∴x2+y2+8y2=36,
∴曲线C2的直角坐标方程为 ![]() =1
=1
(2)解:∵C1上的点P对应的参数为t= ![]() ,∴P(﹣4,4),
,∴P(﹣4,4),
∵Q为C2上的动点,∴Q(6cosθ,2sinθ),
∴PQ中点M(﹣2+3cosθ,2+sinθ),
∵直线C3: ![]() (α为参数),
(α为参数),
∴C3为直线x+ ![]() y+6
y+6 ![]() =0,
=0,
∴点M到C1的距离:
d= ![]() =|4
=|4 ![]() |,
|,
∴当sin( ![]() )=﹣1时,PQ中点M到直线C3:
)=﹣1时,PQ中点M到直线C3: ![]() (α为参数)距离的最小值:
(α为参数)距离的最小值:
dmin=3 ![]() ﹣1
﹣1
【解析】(1)曲线C1的参数方程中利用sin2t+cos2t=1,消去参数t,能求出曲线C1的普通方程;曲线C2的极坐标方程中利用ρ2=x2+y2 , y=ρsinθ,能求出曲线C2的直角坐标方程.(2)先求出P(﹣4,4),Q(6cosθ,2sinθ),从而求出PQ中点M的坐标,再求出直线C3的直角坐标方程,由此利用点到直线的距离公式能求出PQ中点M到直线C3的距离的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
以坐标原点
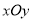 为极点,以
为极点,以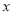 轴正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线
轴正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线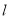 的参数方程为
的参数方程为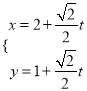 (
(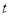 为参数),圆
为参数),圆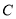 的极坐标方程为
的极坐标方程为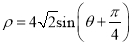 .
.(1)求直线
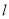 的普通方程与圆
的普通方程与圆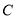 的直角坐标方程;
的直角坐标方程;(2)设圆
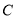 与直线
与直线 交于
交于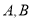 两点,若点
两点,若点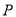 的直角坐标为
的直角坐标为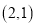 ,求
,求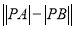 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是定义在R上不恒为0的函数,且对于任意的实数a,b满足f(2)=2,f(ab)=af(b)+bf(a),an=
 (n∈N*),bn=
(n∈N*),bn=  (n∈N*),给出下列命题:
(n∈N*),给出下列命题:
①f(0)=f(1);
②f(x)为奇函数;
③数列{an}为等差数列;
④数列{bn}为等比数列.
其中正确的命题是 . (写出所有正确命题的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】记函数
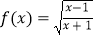 的定义域为A,g(x)=lg[(x﹣a﹣1)(2a﹣x)](a<1)的定义域为B,求
的定义域为A,g(x)=lg[(x﹣a﹣1)(2a﹣x)](a<1)的定义域为B,求
(1)A,B;
(2)若BA,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:2x≤256且log2x≥
 ,
,
(1)求x的取值范围;
(2)求函数log2( )log2(
)log2(  )的最大值和最小值以及相应的x的取值.
)的最大值和最小值以及相应的x的取值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=ax2+2x+c(a≠0),函数f(x)对于任意的都满足条件f(1+x)=f(1﹣x).
(1)若函数f(x)的图象与y轴交于点(0,2),求函数f(x)的解析式;
(2)若函数f(x)在区间(0,1)上有零点,求实数c的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设a>0,
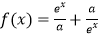 是R上的偶函数.
是R上的偶函数.
(1)求a的值;
(2)证明f(x)在(0,+∞)上为增函数.
相关试题

