【题目】已知![]() 是一元二次方程
是一元二次方程![]() 的两个实数根.
的两个实数根.
(1)是否存在实数![]() ,使
,使![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(2)求使![]() 的值为整数的实数
的值为整数的实数![]() 的整数值.
的整数值.
(3)已知对于x的所有实数值,二次函数![]() 的值都是非负的,求关于x的方程
的值都是非负的,求关于x的方程![]() 的根的取值范围
的根的取值范围
参考答案:
【答案】(1)不存在实数![]() (2)
(2)![]() (3)
(3)![]()
【解析】
试题分析:(1)根据已知方程有两个实数根,那么△≥0,可得k的范围,由于方程有两个实数根,那么根据根与系数的关系可得![]() ,然后把
,然后把![]() 代入
代入![]() 中,进而可求k的值;(2)由
中,进而可求k的值;(2)由![]() 是一元二次方程4kx2-4kx+k+2=0的两个实数根,利用根与系数的关系表示出
是一元二次方程4kx2-4kx+k+2=0的两个实数根,利用根与系数的关系表示出![]() ,将
,将![]() 通分并利用同分母分式的加法法则计算,利用完全平方公式变形后,把表示出
通分并利用同分母分式的加法法则计算,利用完全平方公式变形后,把表示出![]() 代入,整理后根据此式子的值为整数,即可求出实数k的整数值;(3)先根据
代入,整理后根据此式子的值为整数,即可求出实数k的整数值;(3)先根据![]() 的值都是非负的,判别式小于等于0求得a的范围,进而根据a的范围确定函数x的解析式,根据函数的单调性求得函数的值域
的值都是非负的,判别式小于等于0求得a的范围,进而根据a的范围确定函数x的解析式,根据函数的单调性求得函数的值域
试题解析:(1)假设存在实数![]() ,使
,使![]() 成立.
成立.
∵ 一元二次方程![]() 的两个实数根
的两个实数根
∴  ,
,
又![]() 是一元二次方程
是一元二次方程![]() 的两个实数根
的两个实数根
∴ 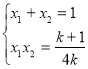
∴![]()
![]() ,但
,但![]() .
.
∴不存在实数![]() ,使
,使![]() 成立.
成立.
(2)∵ ![]()
∴ 要使其值是整数,只需![]() 能被4整除,故
能被4整除,故![]() ,注意到
,注意到![]() ,
,
故要使![]() 的值为整数的实数
的值为整数的实数![]() 的整数值为
的整数值为![]() .
.
(3)![]() 的图像开口向上
的图像开口向上
要![]() 的值都是非负
的值都是非负
即![]()
![]() -
-
①当![]() 时
时
![]()
![]()
![]()
![]()
当![]() 时
时
![]() 的最大值等于
的最大值等于![]()
当![]() 时
时
![]() 的最小值等于
的最小值等于![]()
②当![]() 时
时
![]()
![]()
![]() =
=
当![]() 时
时
![]() 的最小值等于6
的最小值等于6
当![]() 时
时
![]() 的最大值等于12
的最大值等于12
综上所述,![]() 的取值范围是
的取值范围是![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
 的底面为直角梯形,
的底面为直角梯形, ,
, 底面
底面 ,且
,且 ,
, 是
是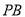 的中点.
的中点.
(1)证明:面
 面
面 ;
;(2)求直线
 与
与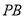 所成角的余弦值;
所成角的余弦值;(3)求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】两平行线分别经过点A(5,0),B(0,12),它们之间的距离d满足的条件是( )
A.0<d≤5
B.0<d≤13
C.0<d<12
D.5≤d≤12 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求函数
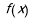 的极值;
的极值;(2)设函数
 ,若对
,若对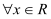 ,
, 恒不小于
恒不小于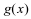 ,求
,求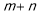 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(用数字作答)从5本不同的故事书和4本不同的数学书中选出4本,送给4位同学,每人1本,问:
(1)如果故事书和数学书各选2本,共有多少种不同的送法?
(2)如果故事书甲和数学书乙必须送出,共有多少种不同的送法?
(3)如果选出的4本书中至少有3本故事书,共有多少种不同的送法?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 ,设
,设 为椭圆上一点,且
为椭圆上一点,且
 .
.(Ⅰ)求
 ;
;(Ⅱ)若
 ,
, ,是否存在以
,是否存在以 为直角顶点的内接于椭圆的等腰直角三角形?若存在,请求出共有几个?若不存在,请说明理由.
为直角顶点的内接于椭圆的等腰直角三角形?若存在,请求出共有几个?若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于定义在区间
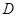 上的函数
上的函数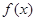 ,若存在闭区间
,若存在闭区间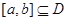 和常数
和常数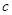 ,使得对任意
,使得对任意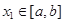 ,都有
,都有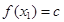 ,且对任意
,且对任意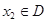 ,当
,当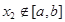 时,
时,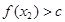 恒成立,则称函数
恒成立,则称函数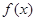 为区间
为区间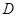 上的“平底型”函数.
上的“平底型”函数.(1)判断函数
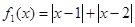 和
和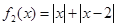 是否为
是否为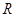 上的“平底型”函数?
上的“平底型”函数?(2)若函数
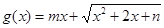 是区间
是区间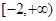 上的“平底型”函数,求
上的“平底型”函数,求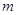 和
和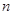 的值.
的值.
相关试题

