【题目】对于定义在区间![]() 上的函数
上的函数![]() ,若存在闭区间
,若存在闭区间![]() 和常数
和常数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,且对任意
,且对任意![]() ,当
,当![]() 时,
时,![]() 恒成立,则称函数
恒成立,则称函数![]() 为区间
为区间![]() 上的“平底型”函数.
上的“平底型”函数.
(1)判断函数![]() 和
和![]() 是否为
是否为![]() 上的“平底型”函数?
上的“平底型”函数?
(2)若函数![]() 是区间
是区间![]() 上的“平底型”函数,求
上的“平底型”函数,求![]() 和
和![]() 的值.
的值.
参考答案:
【答案】(1)不是“平底型”函数.(2)![]()
【解析】试题分析:(1)分区间去掉绝对值符号,分别讨论![]() 与
与![]() 的性质与“平底型”函数定义对照即可;
的性质与“平底型”函数定义对照即可;
(2) 函数![]() 是区间
是区间![]() 上的“平底型”函数等价于存在区间
上的“平底型”函数等价于存在区间![]() 和常数
和常数![]() ,使得
,使得![]() 恒成立,即
恒成立,即![]() 恒成立,亦即
恒成立,亦即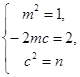 ,解之即可.
,解之即可.
试题解析: (1)对于函数![]() ,当
,当![]() 时,
时,![]() .
.
当![]() 或
或![]() 时,
时,![]() 恒成立,故
恒成立,故![]() 是“平底型”函数.
是“平底型”函数.
对于函数![]() ,当
,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
所以不存在闭区间![]() ,使当
,使当![]() 时,
时,![]() 恒成立,故
恒成立,故![]() 不是“平底型”函数.
不是“平底型”函数.
(2)因为函数![]() 是区间
是区间![]() 上的“平底型”函数,则
上的“平底型”函数,则
存在区间![]() 和常数
和常数![]() ,使得
,使得![]() 恒成立.
恒成立.
所以![]() 恒成立,即
恒成立,即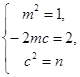 解得
解得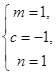 或
或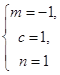 .
.
当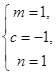 时,
时,![]() .当
.当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 恒成立,此时,
恒成立,此时,![]() 是区间
是区间![]() 上的“平底型”函数.
上的“平底型”函数.
当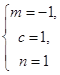 时,
时,![]() .当
.当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 恒成立,此时,
恒成立,此时,![]() 不是区间
不是区间![]() 上的“平底型”函数.
上的“平底型”函数.
综上分析,![]() 为所求.
为所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是一元二次方程
是一元二次方程 的两个实数根.
的两个实数根.(1)是否存在实数
 ,使
,使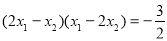 成立?若存在,求出
成立?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(2)求使
 的值为整数的实数
的值为整数的实数 的整数值.
的整数值.(3)已知对于x的所有实数值,二次函数
 的值都是非负的,求关于x的方程
的值都是非负的,求关于x的方程 的根的取值范围
的根的取值范围 -
科目: 来源: 题型:
查看答案和解析>>【题目】(用数字作答)从5本不同的故事书和4本不同的数学书中选出4本,送给4位同学,每人1本,问:
(1)如果故事书和数学书各选2本,共有多少种不同的送法?
(2)如果故事书甲和数学书乙必须送出,共有多少种不同的送法?
(3)如果选出的4本书中至少有3本故事书,共有多少种不同的送法?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 ,设
,设 为椭圆上一点,且
为椭圆上一点,且
 .
.(Ⅰ)求
 ;
;(Ⅱ)若
 ,
, ,是否存在以
,是否存在以 为直角顶点的内接于椭圆的等腰直角三角形?若存在,请求出共有几个?若不存在,请说明理由.
为直角顶点的内接于椭圆的等腰直角三角形?若存在,请求出共有几个?若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于定义在区间
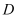 上的函数
上的函数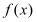 ,若存在闭区间
,若存在闭区间 和常数
和常数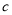 ,使得对任意
,使得对任意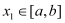 ,都有
,都有 ,且对任意
,且对任意 ,当
,当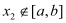 时,
时, 恒成立,则称函数
恒成立,则称函数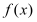 为区间
为区间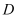 上的“平底型”函数.
上的“平底型”函数.(1)判断函数
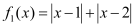 和
和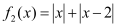 是否为
是否为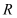 上的“平底型”函数?
上的“平底型”函数?(2)若函数
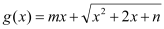 是区间
是区间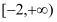 上的“平底型”函数,求
上的“平底型”函数,求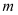 和
和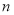 的值.
的值. -
科目: 来源: 题型:
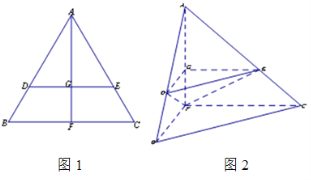
查看答案和解析>>【题目】如图1,在边长为1的等边三角形
 中,
中,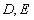 分别是
分别是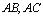 边上的点,
边上的点, ,
, 是
是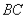 的中点,
的中点, 与
与 交于点
交于点 ,将
,将 沿
沿 折起,得到如图2所示的三棱锥
折起,得到如图2所示的三棱锥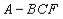 ,其中
,其中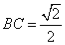 .
.
(1) 证明:
 //平面
//平面 ;
; (2) 证明:
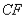
 平面
平面 ;
;(3) 当
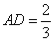 时,求三棱锥
时,求三棱锥 的体积
的体积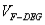 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】利用输入语句可以给多个变量赋值,下面能实现这一功能的语句是( )
A.INPUT “A,B,C”a,b,c
B.INPUT “A,B,C=”;a,b,c
C.INPUT a,b,c;“A,B,C”
D.PRINT “A,B,C”;a,b,c
相关试题

