【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,若
时,若![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的值;
的值;
(3)求证:![]() .
.
参考答案:
【答案】(1)![]() 时,
时,![]() 的单调递增区间是
的单调递增区间是![]() ,
,![]() 时,
时,![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题分析:(1)先求导函数数,利用![]() ,即可求函数
,即可求函数![]() 的单调增区间,
的单调增区间,![]() 即可求函数
即可求函数![]() 的单调减区间;(2)若
的单调减区间;(2)若![]() 对任意的
对任意的![]() 恒成立,
恒成立,![]() 对
对![]() 恒成立, 即可求实数
恒成立, 即可求实数![]() 的值;(3)要证原不等式成立,只需证:
的值;(3)要证原不等式成立,只需证: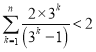 ,即证:
,即证: 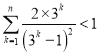 ,结合(2)利用裂项相消法求和,根据放缩法可证.
,结合(2)利用裂项相消法求和,根据放缩法可证.
试题解析:解:(1)![]() ,∴
,∴![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增:
上单调递增:![]() 时,
时,![]() 时,
时,![]() 单调递减,
单调递减,![]() 时,
时,![]() 单调递增.
单调递增.
(2)由(1),![]() 时,
时,![]() ,∴
,∴![]() ,即
,即![]() ,
,
记![]() .
.![]() ,∴
,∴![]() 在
在![]() 上增,在
上增,在![]() 上递减,∴
上递减,∴![]() ,故
,故![]() ,得
,得![]() .
.
(3)![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
![]() 时,
时,![]() .
.
由(2)可知![]() ,即
,即![]() ,则
,则![]() 时,
时,![]() ,故
,故![]() ,
,
即原不等式成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 满足
满足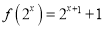 ,定义数列
,定义数列 ,
,  ,
,  ,数列
,数列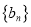 的前
的前 项和为
项和为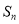 ,
,  ,且
,且 .
.(1) 求数列
 、
、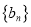 的通项公式;
的通项公式;(2)令
 ,求
,求 的前
的前 项和
项和 ;
;(3)数列
 中是否存在三项
中是否存在三项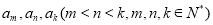 使
使 成等差数列,若存在,求出
成等差数列,若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在坐标原点,焦点在
 轴上的椭圆,离心率为
轴上的椭圆,离心率为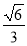 且过点
且过点 ,过定点
,过定点 的动直线与该椭圆相交于
的动直线与该椭圆相交于 两点.
两点.(1)若线段
 中点的横坐标是
中点的横坐标是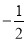 ,求直线
,求直线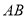 的方程;
的方程;(2)在
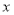 轴上是否存在点
轴上是否存在点 ,使
,使 为常数?若存在,求出点
为常数?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂以
 千克/小时的速度匀速生产某种产品(生产条件要求
千克/小时的速度匀速生产某种产品(生产条件要求 ),每一小时可获得的利润是
),每一小时可获得的利润是 元.
元.(1)要使生产该产品2小时获得的利润不低于1500元,求
 的取值范围;
的取值范围;(2) 要使生产480千克该产品获得的利润最大,问:该厂应该选取何种生产速度?并求此最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知圆C:(x﹣2)2+(y+1)2=5,过点P(5,0)且斜率为k的直线
 与圆C相交于不同的两点A,B.
与圆C相交于不同的两点A,B.(I)求k的取值范围;
(Ⅱ)若弦长|AB|=4,求直线
 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了准确地调查我国某一时期的人口总量、人口分布、民族人口、城乡人口、受教育的程度、迁徙流动、就业状况等多方面的情况,需要用______的方法进行调查.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 为实数,且
为实数,且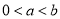 ,
,(1)求方程
 的解; (2)若
的解; (2)若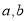 满足
满足 ,求证:①
,求证:① ②
② ; (3)在(2)的条件下,求证:由关系式
; (3)在(2)的条件下,求证:由关系式 所得到的关于
所得到的关于 的方程
的方程 存在
存在 ,使
,使
相关试题

