【题目】已知中心在坐标原点,焦点在![]() 轴上的椭圆,离心率为
轴上的椭圆,离心率为![]() 且过点
且过点![]() ,过定点
,过定点![]() 的动直线与该椭圆相交于
的动直线与该椭圆相交于![]() 两点.
两点.
(1)若线段![]() 中点的横坐标是
中点的横坐标是![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为常数?若存在,求出点
为常数?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)椭圆的离心率公式,及![]() 的关系,求得
的关系,求得![]() ,得到椭圆的方程;设出直线
,得到椭圆的方程;设出直线![]() 的方程,将直线方程代入椭圆,用舍而不求和韦达定理方法表示出中点坐标,此时代入已知
的方程,将直线方程代入椭圆,用舍而不求和韦达定理方法表示出中点坐标,此时代入已知![]() 中点的横坐标,即可求出直线
中点的横坐标,即可求出直线![]() 的方程;(2)假设存在点
的方程;(2)假设存在点![]() ,使
,使![]() 为常数,分别分当
为常数,分别分当![]() 与
与![]() 轴不垂直时以及当直线
轴不垂直时以及当直线![]() 与
与![]() 轴垂直时,求出点
轴垂直时,求出点![]() 的坐标,最后综合两种情况得出结论.
的坐标,最后综合两种情况得出结论.
试题解析:(1)易求椭圆的方程为![]() ,
,
直线斜率不存在时显然不成立,设直线![]() ,
,
将![]() 代入椭圆的方程
代入椭圆的方程![]() ,
,
消去![]() 整理得
整理得![]() ,
,
设![]() ,则
,则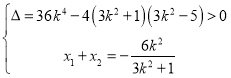 ,
,
因为线段![]() 的中点的横坐标为
的中点的横坐标为![]() ,解得
,解得![]() ,
,
所以直线![]() 的方程为
的方程为![]() .
.
(2)假设在![]() 轴上存在点
轴上存在点![]() ,使得
,使得![]() 为常数,
为常数,
①当直线![]() 与
与![]() 轴不垂直时,由(1)知
轴不垂直时,由(1)知![]() ,
,
所以![]()
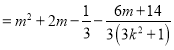 ,
,
因为![]() 是与
是与![]() 无关的常数,从而有
无关的常数,从而有![]() ,
,
此时![]()
②当直线![]() 与
与![]() 轴垂直时,此时结论成立,
轴垂直时,此时结论成立,
综上可知,在![]() 轴上存在定点
轴上存在定点![]() ,使
,使![]() ,为常数
,为常数
-
科目: 来源: 题型:
查看答案和解析>>【题目】某制造厂商10月份生产了一批乒乓球,从中随机抽取
 个进行检查,测得每个球的直径(单位:
个进行检查,测得每个球的直径(单位: ),将数据进行分组,得到如下频率分布表:
),将数据进行分组,得到如下频率分布表:
(1)求
 、
、 、
、 及
及 、
、 的值,并画出频率分布直方图(结果保留两位小数);
的值,并画出频率分布直方图(结果保留两位小数);(2)已知标准乒乓球的直径为
 ,直径误差不超过
,直径误差不超过 的为五星乒乓球,若这批乒乓球共有
的为五星乒乓球,若这批乒乓球共有 个,试估计其中五星乒乓球的数目;
个,试估计其中五星乒乓球的数目;(3)统计方法中,同一组数据常用该组区间的中点值(例如区间
 的中点值是
的中点值是 )作为代表,估计这批乒乓球直径的平均值和中位数.
)作为代表,估计这批乒乓球直径的平均值和中位数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在坐标原点,焦点在
 轴上的椭圆,离心率为
轴上的椭圆,离心率为 且过点
且过点 ,过定点
,过定点 的动直线与该椭圆相交于
的动直线与该椭圆相交于 、
、 两点.
两点.(1)若线段
 中点的横坐标是
中点的横坐标是 ,求直线
,求直线 的方程;
的方程;(2)在
 轴上是否存在点
轴上是否存在点 ,使
,使 为常数?若存在,求出点
为常数?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 满足
满足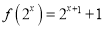 ,定义数列
,定义数列 ,
,  ,
,  ,数列
,数列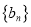 的前
的前 项和为
项和为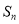 ,
,  ,且
,且 .
.(1) 求数列
 、
、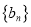 的通项公式;
的通项公式;(2)令
 ,求
,求 的前
的前 项和
项和 ;
;(3)数列
 中是否存在三项
中是否存在三项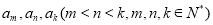 使
使 成等差数列,若存在,求出
成等差数列,若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂以
 千克/小时的速度匀速生产某种产品(生产条件要求
千克/小时的速度匀速生产某种产品(生产条件要求 ),每一小时可获得的利润是
),每一小时可获得的利润是 元.
元.(1)要使生产该产品2小时获得的利润不低于1500元,求
 的取值范围;
的取值范围;(2) 要使生产480千克该产品获得的利润最大,问:该厂应该选取何种生产速度?并求此最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( 为自然对数的底数).
为自然对数的底数).(1)求函数
 的单调区间;
的单调区间;(2)当
 时,若
时,若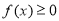 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的值;
的值;(3)求证:
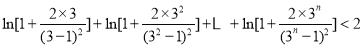 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知圆C:(x﹣2)2+(y+1)2=5,过点P(5,0)且斜率为k的直线
 与圆C相交于不同的两点A,B.
与圆C相交于不同的两点A,B.(I)求k的取值范围;
(Ⅱ)若弦长|AB|=4,求直线
 的方程.
的方程.
相关试题

