【题目】设![]() 为实数,且
为实数,且![]() ,
,
(1)求方程![]() 的解; (2)若
的解; (2)若![]() 满足
满足![]() ,求证:①
,求证:①![]() ②
②![]() ; (3)在(2)的条件下,求证:由关系式
; (3)在(2)的条件下,求证:由关系式![]() 所得到的关于
所得到的关于![]() 的方程
的方程![]() 存在
存在![]() ,使
,使![]()
参考答案:
【答案】(1) ![]() 或
或![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】试题分析:(1)令![]() 即
即![]() ,故
,故![]() .(2)①由于
.(2)①由于![]() ,故
,故![]() ,也即
,也即![]() ,所以
,所以![]() , ②由(1)可化简
, ②由(1)可化简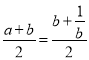 ,令
,令![]() ,利用单调性的定义证明函数在区间
,利用单调性的定义证明函数在区间![]() 上为增函数,由此证得
上为增函数,由此证得![]() .(3)化简关系式得到
.(3)化简关系式得到![]() ,即
,即![]() ,利用
,利用![]() 消去
消去![]() ,得到关于
,得到关于![]() 的方程,利用二分法可判断零点在区间
的方程,利用二分法可判断零点在区间![]() .
.
试题解析:
由![]() ,得
,得![]() 所以
所以![]() 或
或![]()
(2)证明:①因为![]() ,且
,且![]() ,可判断
,可判断![]() ,
, ![]()
所以![]() ,即
,即![]() 即
即![]() ,则
,则![]()
②由①得 令
令![]() ,(
,( ![]() )
)
任取![]() 且
且![]()
因为![]()
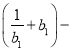

=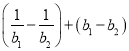 =
=![]() =
=![]()

![]()
![]()
![]()
![]() 在
在![]() 上为增函数,
上为增函数,
![]() ,
, ![]()
(3)证明: ![]()
![]()
![]()
![]() ,得
,得![]() 又
又![]()
![]() .
.
令![]()
![]() ,因为
,因为![]()
根据函数零点的判断条件可知,函数![]() 在(3,4)内一定存在零点,
在(3,4)内一定存在零点,
即存在![]() 使
使![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( 为自然对数的底数).
为自然对数的底数).(1)求函数
 的单调区间;
的单调区间;(2)当
 时,若
时,若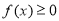 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的值;
的值;(3)求证:
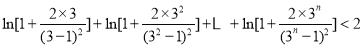 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知圆C:(x﹣2)2+(y+1)2=5,过点P(5,0)且斜率为k的直线
 与圆C相交于不同的两点A,B.
与圆C相交于不同的两点A,B.(I)求k的取值范围;
(Ⅱ)若弦长|AB|=4,求直线
 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了准确地调查我国某一时期的人口总量、人口分布、民族人口、城乡人口、受教育的程度、迁徙流动、就业状况等多方面的情况,需要用______的方法进行调查.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次篮球定点投篮训练中,规定每人最多投3次,在
 处每投进一球得3分;在
处每投进一球得3分;在 处每投进一球得2分.如果前两次得分之和超过3分就停止投篮;否则投第三次.某同学在
处每投进一球得2分.如果前两次得分之和超过3分就停止投篮;否则投第三次.某同学在 处的投中率
处的投中率 ,在
,在 处的投中率为
处的投中率为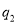 ,该同学选择先在
,该同学选择先在 处投第一球,以后都在
处投第一球,以后都在 处投,且每次投篮都互不影响,用
处投,且每次投篮都互不影响,用 表示该同学投篮训练结束后所得的总分,其分布列为:
表示该同学投篮训练结束后所得的总分,其分布列为:
0
2
3
4
5

0.03




(1)求
 的值;
的值;(2)求随机变量
 的数学期望
的数学期望 ;
;(3)试比较该同学选择上述方式投篮得分超过3分与选择都在
 处投篮得分超过3分的概率的大小.
处投篮得分超过3分的概率的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市经营一批产品,在市场销售中发现此产品在30天内的日销售量P(件)与日期
 )之间满足
)之间满足 ,已知第5日的销售量为55件,第10日的销售量为50件。
,已知第5日的销售量为55件,第10日的销售量为50件。(1)求第20日的销售量; (2)若销售单价Q(元/件)与
 的关系式为
的关系式为 ,求日销售额
,求日销售额 的最大值。
的最大值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】脱贫是政府关注民生的重要任务,了解居民的实际收入状况就显得尤为重要.现从某地区随机抽取
 个农户,考察每个农户的年收入与年积蓄的情况进行分析,设第
个农户,考察每个农户的年收入与年积蓄的情况进行分析,设第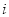 个农户的年收入
个农户的年收入 (万元),年积蓄
(万元),年积蓄 (万元),经过数据处理得
(万元),经过数据处理得
(Ⅰ)已知家庭的年结余
 对年收入
对年收入 具有线性相关关系,求线性回归方程;
具有线性相关关系,求线性回归方程;(Ⅱ)若该地区的农户年积蓄在
 万以上,即称该农户已达小康生活,请预测农户达到小康生活的最低年收入应为多少万元?
万以上,即称该农户已达小康生活,请预测农户达到小康生活的最低年收入应为多少万元?附:在
 中,
中, 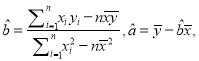 其中
其中 为样本平均值.
为样本平均值.
相关试题

