搜索
【题目】已知函数f（x）=x3+2x2﹣ax+1在区间（﹣1，1）上恰有一个极值点，则实数a的取值范围是 ．
参考答案：
【答案】﹣1≤a＜7
【解析】
试题分析：首先利用函数的导数与极值的关系求出a的值，由于函数f（x）=x3+2x2﹣ax+1在区间（﹣1，1）上恰有一个极值点，所以f′（﹣1）f′（1）＜0，进而验证a=﹣1与a=7时是否符合题意，即可求答案．
解：由题意，f′（x）=3x2+4x﹣a，
当f′（﹣1）f′（1）＜0时，函数f（x）=x3+2x2﹣ax+1在区间（﹣1，1）上恰有一个极值点，
解得﹣1＜a＜7，
当a=﹣1时，f′（x）=3x2+4x+1=0，在（﹣1，1）上恰有一根x=﹣
，
当a=7时，f′（x）=3x2+4x﹣7=0在（﹣1，1）上无实根，
则a的取值范围是﹣1≤a＜7，
故答案为﹣1≤a＜7．
-
科目： 来源： 题型：
查看答案和解析>>【题目】运行如图所示的程序框图，则输出结果为（ ）
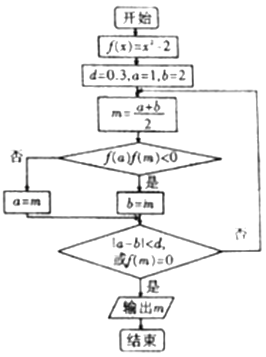
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=（2﹣a）（x﹣1）﹣2lnx
（1）当a=1时，求f（x）的单调区间；
（2）若函数f（x）在（0，
）上无零点，求a最小值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知向量
， 
， 
（m＞0，n＞0），若m+n∈[1，2]，则 
的取值范围是（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知{an}是首项为19，公差为－2的等差数列，Sn为{an}的前n项和．
(1)求通项an及Sn；
(2)设{bn－an}是首项为1，公比为3的等比数列，求数列{bn}的通项公式及前n项和Tn.
-
科目： 来源： 题型：
查看答案和解析>>【题目】（本题满分12分）已知不等式ax2－3x＋6>4的解集为{x|x<1或x>b}，
（1）求a，b；
（2）解不等式ax2－（ac＋b）x＋bc<0.
-
科目： 来源： 题型：
查看答案和解析>>【题目】设a>0且a≠1，函数f(x)＝
x2－(a＋1)x＋alnx.(1)当a＝2时，求曲线y＝f(x)在(3，f(3))处切线的斜率；
(2)求函数f(x)的极值点．
相关试题
