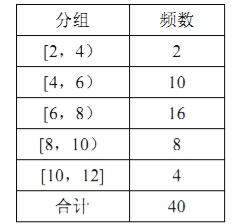
【题目】从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.
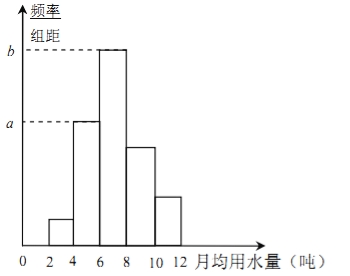
(1)求频率分布直方图中![]() 的值;
的值;
(2)从该小区随机选取一个家庭,试估计这个家庭去年的月均用水量不低于6吨的概率;
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,将该样本看成一个总体,从中任意选取2个家庭,求其中恰有一个家庭的月均用水量不低于8吨的概率.
参考答案:
【答案】(1)![]() ;(2)0.7;(3)
;(2)0.7;(3)![]() .
.
【解析】
试题分析:(1)利用频率分布直方图中小矩形的高的实际意义进行求解;(2)利用频率来估计概率;(3)先利用分层抽样得到各层抽得的人数,列举出所有基本事件和满足要求的基本事件,再利用古典概型的概率公式进行求解.
试题解析:(1)因为样本中家庭月均用水量在![]() 上的频率为
上的频率为![]() ,
,
在![]() 上的频率为
上的频率为![]() ,
,
所以![]() ,
,![]() .………………2分
.………………2分
(2)根据频数分布表,40个家庭中月均用水量不低于6吨的家庭共有16+8+4=28个,
所以样本中家庭月均用水量不低于6吨的概率是![]() .
.
利用样本估计总体,从该小区随机选取一个家庭,可估计这个家庭去年的月均用水量不低于6吨的概率约为0.7.………………4分
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,
则在![]() 上应抽取
上应抽取![]() 人,记为
人,记为![]() ,………………5分
,………………5分
在![]() 上应抽取
上应抽取![]() 人,记为
人,记为![]() ,………………6分
,………………6分
在![]() 上应抽取
上应抽取![]() 人,记为
人,记为![]() .………………7分
.………………7分
设“从中任意选取2个家庭,求其中恰有1个家庭的月均用水量不低于8吨”为事件,
则所有基本事件有:![]()
![]()
![]()
![]() ,共21种.…………9分
,共21种.…………9分
事件包含的基本事件有:![]() ,
,
![]()
![]()
![]() 共12种.………………11分
共12种.………………11分
所以其中恰有一个家庭的月均用水量不低于8吨的概率为![]() .………………12分
.………………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
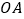 、
、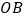 是两条公路(近似看成两条直线),
是两条公路(近似看成两条直线),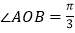 ,在
,在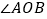 内有一纪念塔
内有一纪念塔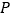 (大小忽略不计),已知
(大小忽略不计),已知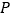 到直线
到直线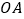 、
、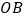 的距离分别为
的距离分别为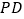 、
、 ,
,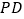 =6千米,
=6千米, =12千米.现经过纪念塔
=12千米.现经过纪念塔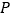 修建一条直线型小路,与两条公路
修建一条直线型小路,与两条公路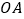 、
、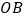 分别交于点
分别交于点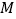 、
、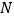 .
.(1)求纪念塔
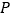 到两条公路交点
到两条公路交点 处的距离;
处的距离;(2)若纪念塔
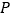 为小路
为小路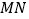 的中点,求小路
的中点,求小路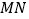 的长.
的长.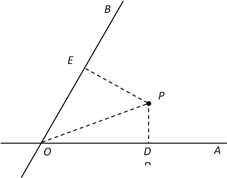
-
科目: 来源: 题型:
查看答案和解析>>【题目】为推行“微课、翻转课堂”教学法,某数学老师分别用传统教学和“微课、翻转课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验,为了比较教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,结果如下表:
记成绩不低于70分者为“成绩优良”.

(1)由以上统计数据填写下面
 列联表,并判断“成绩优良与教学方式是否有关”?
列联表,并判断“成绩优良与教学方式是否有关”?
附:
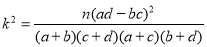
临界值表:

(2)现从上述40人中,学校按成绩是否优良采用分层抽样的方法抽取8人进行考核,在这8人中,记成绩不优良的乙班人数为
 ,求
,求 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
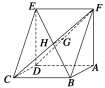
(1)求证:GH∥平面CDE;
(2)若CD=2,DB=4
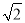 ,求四棱锥F—ABCD的体积.
,求四棱锥F—ABCD的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国的高铁技术发展迅速,铁道部门计划在
 两城市之间开通高速列车,假设列车在试运行期间,每天在
两城市之间开通高速列车,假设列车在试运行期间,每天在 两个时间段内各发一趟由
两个时间段内各发一趟由 城开往
城开往 城的列车(两车发车情况互不影响),
城的列车(两车发车情况互不影响), 城发车时间及概率如下表所示:
城发车时间及概率如下表所示:发车
时间






概率






若甲、乙两位旅客打算从
 城到
城到 城,他们到达
城,他们到达 火车站的时间分别是周六的
火车站的时间分别是周六的 和周日的
和周日的 (只考虑候车时间,不考虑其他因素).
(只考虑候车时间,不考虑其他因素).(1)设乙候车所需时间为随机变量
 (单位:分钟),求
(单位:分钟),求 的分布列和数学期望
的分布列和数学期望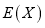 ;
;(2)求甲、乙两人候车时间相等的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在12件同类型的零件中有2件次品,抽取3次进行检验,每次抽取1件,并且取出后不再放回,若以ξ和η分别表示取到的次品数和正品数.
(1)求ξ的分布列、均值和方差;
(2)求η的分布列、均值和方差.
-
科目: 来源: 题型:
查看答案和解析>>【题目】袋中有20个大小相同的球,其中记上0号的有10个,记上n号的有n个(n=1,2,3,4),现从袋中任取一球,X表示所取球的标号.
(1)求X的分布列,均值和方差;
(2)若Y=aX+b,E(Y)=1,D(Y)=11,试求a,b的值.
相关试题

