【题目】已知函数![]() .将
.将![]() 的图象向左平移
的图象向左平移![]() 个单位长度后所得的函数为偶函数,则关于函数
个单位长度后所得的函数为偶函数,则关于函数![]() ,下列命题正确的是( )
,下列命题正确的是( )
A. 函数![]() 在区间
在区间![]() 上有最小值 B. 函数
上有最小值 B. 函数![]() 在区间
在区间![]() 上单调递增
上单调递增
C. 函数![]() 的一条对称轴为
的一条对称轴为![]() D. 函数
D. 函数![]() 的一个对称点为
的一个对称点为![]()
参考答案:
【答案】B
【解析】
分析:求出函数平移后的解析式,由偶函数的性质求出参数![]() ,判断最值、单调区间、对称轴、对称中心时需将结论代入原函数,根据
,判断最值、单调区间、对称轴、对称中心时需将结论代入原函数,根据![]() 的图像与性质判断正确与否.
的图像与性质判断正确与否.
详解:由题意知平移后的解析式为:![]() ,因为此函数为偶函数,
,因为此函数为偶函数,
所以y轴为其对称轴之一,所以将![]() 代入可得
代入可得![]() ,
,
解得:![]() ,由
,由![]() 的取值范围可得
的取值范围可得![]() ,
,
所以原解析式为![]() ,
,
A选项,将区间代入函数,可得![]() ,根据
,根据![]() 图像可知无最值,
图像可知无最值,
B选项,将区间代入函数,可得![]() ,根据
,根据![]() 图像知函数单调递增,
图像知函数单调递增,
C选项,将![]() 代入函数,可得
代入函数,可得![]() ,所以应为对称中心的横坐标,
,所以应为对称中心的横坐标,
D选项,将![]() 代入函数,可得
代入函数,可得![]() ,所以应为对称轴与x轴交点.
,所以应为对称轴与x轴交点.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某省数学学业水平考试成绩共分为
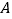 、
、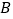 、
、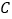 、
、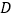 四个等级,在学业水平考试成绩分布后,从该省某地区考生中随机抽取
四个等级,在学业水平考试成绩分布后,从该省某地区考生中随机抽取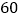 名考生,统计他们的数学成绩,部分数据如下:
名考生,统计他们的数学成绩,部分数据如下:等级
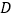
频数
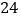
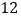
频率
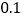
(1)补充完成上述表格的数据;
(2)现按上述四个等级,用分层抽样方法从这
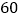 名考生中抽取
名考生中抽取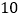 名.在这
名.在这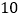 名考生中,从成绩为
名考生中,从成绩为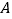 等和
等和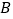 等的所有考生中随机抽取
等的所有考生中随机抽取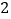 名,求至少有
名,求至少有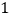 名成绩为
名成绩为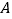 等的概率.
等的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 (
( )与双曲线
)与双曲线 (
( ,
, )有相同的焦点
)有相同的焦点 ,点
,点 是两条曲线的一个交点,且
是两条曲线的一个交点,且 轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是( )
轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】
11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X个球该局比赛结束.
(1)求P(X=2);
(2)求事件“X=4且甲获胜”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,(
,( 为常数),
为常数), .曲线
.曲线 在点
在点 处的切线与
处的切线与 轴平行
轴平行(1)求
 的值;
的值;(2)求
 的单调区间和最小值;
的单调区间和最小值;(3)若
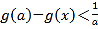 对任意
对任意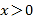 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(2017·全国卷Ⅲ文,18)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温
[10,15)
[15,20)
[20,25)
[25,30)
[30,35)
[35,40)
天数
2
16
36
25
7
4
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
 交付金额(元)
交付金额(元)支付方式
(0,1000]
(1000,2000]
大于2000
仅使用A
18人
9人
3人
仅使用B
10人
14人
1人
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.
相关试题

