【题目】某省数学学业水平考试成绩共分为![]() 、
、![]() 、
、![]() 、
、![]() 四个等级,在学业水平考试成绩分布后,从该省某地区考生中随机抽取
四个等级,在学业水平考试成绩分布后,从该省某地区考生中随机抽取![]() 名考生,统计他们的数学成绩,部分数据如下:
名考生,统计他们的数学成绩,部分数据如下:
等级 |
|
|
|
|
频数 |
|
| ||
频率 |
|
(1)补充完成上述表格的数据;
(2)现按上述四个等级,用分层抽样方法从这![]() 名考生中抽取
名考生中抽取![]() 名.在这
名.在这![]() 名考生中,从成绩为
名考生中,从成绩为![]() 等和
等和![]() 等的所有考生中随机抽取
等的所有考生中随机抽取![]() 名,求至少有
名,求至少有![]() 名成绩为
名成绩为![]() 等的概率.
等的概率.
参考答案:
【答案】(1)见解析(2) ![]()
【解析】
(1)根据频率![]() ,即可求出相应数据;
,即可求出相应数据;
(2)用分层抽样可得A、B分别抽取到的人数为4人、3人,列举可得总的基本事件共21个,由概率公式可得.
(1)
等级 |
|
|
|
|
频数 |
|
|
|
|
频率 |
|
|
|
|
(2)成绩为![]() 等的考生应抽
等的考生应抽![]() 名,分别记为
名,分别记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
成绩为![]() 等的考生应抽
等的考生应抽![]() 名,分别记为
名,分别记为![]() ,
,![]() ,
,![]() ,
,
从这![]() 名中抽取
名中抽取![]() 名,有如下
名,有如下![]() 种抽法:
种抽法:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() .
.
其中至少有![]() 名成绩为
名成绩为![]() 等的有如下
等的有如下![]() 种抽法:
种抽法:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() .
.
∴至少有![]() 名成绩为
名成绩为![]() 等的概率为
等的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
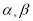 表示两个不同的平面,
表示两个不同的平面, 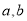 表示两条不同直线,对于下列两个命题:
表示两条不同直线,对于下列两个命题:①若
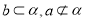 ,则“
,则“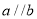 ”是“
”是“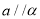 ”的充分不必要条件;
”的充分不必要条件;②若
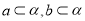 ,则“
,则“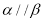 ”是“
”是“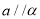 且
且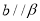 ”的充要条件.判读正确的是( )
”的充要条件.判读正确的是( )A. ①②都是真命题 B. ①是真命题,②是假命题
C. ①是假命题,②是真命题 D. ①②都是假命题
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
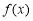 是二次函数,不等式
是二次函数,不等式 的解集为
的解集为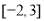 ,且
,且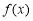 在区间
在区间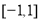 上的最小值是4.
上的最小值是4.(1)求
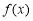 的解析式;
的解析式;(2)求
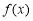 在
在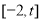 上的最大值
上的最大值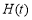 、最小值
、最小值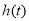 的解析式;
的解析式;(3)设
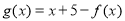 ,若对任意
,若对任意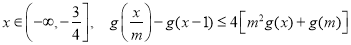 均成立,求实数
均成立,求实数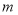 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有
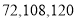 人,现采用分层抽样的方法,从该单位上述员工中抽取
人,现采用分层抽样的方法,从该单位上述员工中抽取 人调查专项附加扣除的享受情况.
人调查专项附加扣除的享受情况.(Ⅰ)应从老、中、青员工中分别抽取多少人?
(Ⅱ)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为
 .享受情况如右表,其中“
.享受情况如右表,其中“ ”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.员工
项目
A
B
C
D
E
F
子女教育
○
○
×
○
×
○
继续教育
×
×
○
×
○
○
大病医疗
×
×
×
○
×
×
住房贷款利息
○
○
×
×
○
○
住房租金
×
×
○
×
×
×
赡养老人
○
○
×
×
×
○
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设
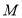 为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件
为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件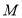 发生的概率.
发生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 (
( )与双曲线
)与双曲线 (
( ,
, )有相同的焦点
)有相同的焦点 ,点
,点 是两条曲线的一个交点,且
是两条曲线的一个交点,且 轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是( )
轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】
11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X个球该局比赛结束.
(1)求P(X=2);
(2)求事件“X=4且甲获胜”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
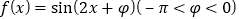 .将
.将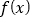 的图象向左平移
的图象向左平移 个单位长度后所得的函数为偶函数,则关于函数
个单位长度后所得的函数为偶函数,则关于函数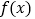 ,下列命题正确的是( )
,下列命题正确的是( )A. 函数
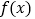 在区间
在区间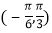 上有最小值 B. 函数
上有最小值 B. 函数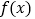 在区间
在区间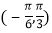 上单调递增
上单调递增C. 函数
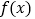 的一条对称轴为
的一条对称轴为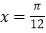 D. 函数
D. 函数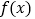 的一个对称点为
的一个对称点为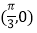
相关试题

