【题目】如图所示, 四棱锥![]() 底面是直角梯形,
底面是直角梯形, ![]() 底面
底面![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() .
.
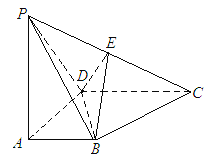
(Ⅰ)证明: ![]() ;
;
(Ⅱ)证明: ![]() ;
;
(Ⅲ)求三棱锥![]() 的体积.
的体积.
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】试题分析:
(1)由题意可证得![]() ,结合线面平行的判断定理即可证得
,结合线面平行的判断定理即可证得![]() ;
;
(2)利用题意结合线面垂直的判断定理即可证得题中的结论;
(3)转化顶点可得四棱锥的体积为![]() .
.
试题解析:
(1)取PD中点Q, 连EQ , AQ ,
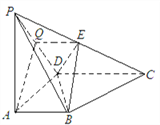
则![]()
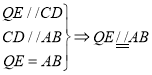
![]()

(2)证明:
PA⊥平面ABCD,CD平面ABCD
PA⊥CD,
又∵CD⊥AD,PA∩AD=A
∴CD⊥平面PAD
又∵AQ平面PAD
∴AQ⊥CD,
又∵PA=AD,Q为PD的中点
∴AQ⊥PD,
又∵PD∩CD=D
AQ⊥平面PCD,BE∥AQ
BE⊥平面PCD.
(3)![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 的定义域为(-1,1),满足f(-x)=-f(x),且
的定义域为(-1,1),满足f(-x)=-f(x),且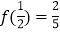 .
. (1)求函数f(x)的解析式;
(2)证明f(x)在(-1,1)上是增函数;
(3)解不等式
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
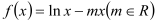 .
.(Ⅰ)讨论函数
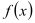 的单调区间.
的单调区间.(Ⅱ)当
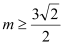 时,设
时,设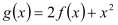 的两个极值点
的两个极值点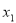 ,
,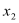
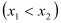 恰为
恰为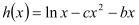 的零点,求
的零点,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
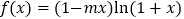 .
.(1)若当
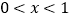 时,函数
时,函数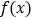 的图象恒在直线
的图象恒在直线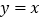 上方,求实数
上方,求实数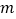 的取值范围;
的取值范围;(2)求证:
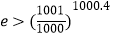 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】近年来我国电子商务行业迎来篷勃发展的新机遇,2016年双11期间,某购物平台的销售业绩高达一千多亿人民币.与此同时,相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(Ⅰ)请完成如下列联表;
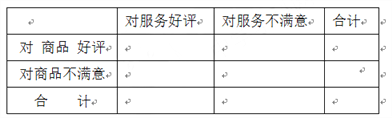
(Ⅱ)是否可以在犯错误的概率不超过0.1%的前提下,认为商品好评与服务好评有关?
(Ⅲ)若针对商品的好评率,采用分层抽样的方式从这200次交易中取出5次交易,并从中选择两次交易进行客户回访,求只有一次好评的概率.

(
 ,其中
,其中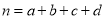 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

(1)证明:函数
 是偶函数;
是偶函数;(2)利用绝对值及分段函数知识,将函数解析式写成分段函数的形式,然后画出函数图像(草图),并写出函数的值域;
(3)在同一坐标系中画出直线
 ,观察图像写出不等式
,观察图像写出不等式 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】北京时间3月15日下午,谷歌围棋人工智能
 与韩国棋手李世石进行最后一轮较量,
与韩国棋手李世石进行最后一轮较量, 获得本场比赛胜利,最终人机大战总比分定格在
获得本场比赛胜利,最终人机大战总比分定格在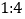 .人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.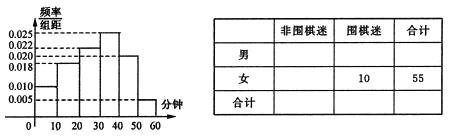
(1)根据已知条件完成如图列联表,并据此资料判断你是否有
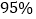 的把握认为“围棋迷”与性别有关?
的把握认为“围棋迷”与性别有关?(2)将上述调查所得到的频率视为概率.现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记所抽取的3名学生中的“围棋迷”人数为
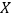 .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求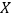 的分布列,期望
的分布列,期望 和方差
和方差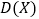 .
.附:
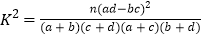 ,其中
,其中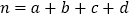 .
.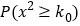
0.05
0.010
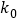
3.74
6.63
相关试题

