【题目】在正方体ABCD-A1B1C1D中,M为DD1的中点,O为AC的中点,AB=2.

(I)求证:BD1∥平面ACM;
(Ⅱ)求证:B1O⊥平面ACM;
(Ⅲ)求三棱锥O-AB1M的体积.
参考答案:
【答案】(Ⅰ)(Ⅱ)详见解析;(Ⅲ)![]() .
.
【解析】
试题分析:(Ⅰ)要证明线面平行,可先证明线线平行,连接BD,MO,根据三角形中位线的平行关系可证明![]() ;(Ⅱ)要证明线面垂直,根据判定定理,可证明线与平面内的两条相交直线垂直,即证明
;(Ⅱ)要证明线面垂直,根据判定定理,可证明线与平面内的两条相交直线垂直,即证明![]() 和
和![]() ;(Ⅲ)将四面体的体积转化为以三角形
;(Ⅲ)将四面体的体积转化为以三角形![]() 当底面,AO是四面体的高的几何体的体积,这样易计算四面体的体积.
当底面,AO是四面体的高的几何体的体积,这样易计算四面体的体积.
试题解析:(I)证明:
连结BD,设BD与AC的交点为O,
∵AC,BD为正方形的对角线,故O为BD中点;
连结MO,
∵O,M分别为DB,DD1的中点,
∴OM∥BD1,…(2分)
∵OM平面ACM,BD1平面ACM…(3分)
∴BD1∥平面ACM. …(4分)
(II)∵AC⊥BD,DD1⊥平面ABCD,且AC平面ABCD,
∴AC⊥DD1;且BD∩DD1=D,∴AC⊥平面BDD1B1…(6分)
OB1平面BDD1B1,∴B1O⊥AC,…(7分)
连结B1M,在△B1MO中 ![]()
∴![]()
∴B1O⊥OM…(10分)
又OM∩AC=O,∴B1O⊥平面AMC; …(11分)
.(II) V=![]()

-
科目: 来源: 题型:
查看答案和解析>>【题目】在单调递增数列
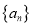 中,
中, 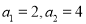 ,且
,且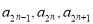 成等差数列,
成等差数列, 成等比数列,
成等比数列,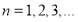 .
. (1)①求证:数列
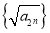 为等差数列;
为等差数列;②求数列
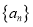 通项公式;
通项公式;(2)设数列
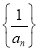 的前
的前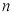 项和为
项和为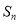 ,证明:
,证明: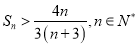 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系中, 以坐标原点
 为极点,
为极点,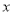 轴的非负半轴为极轴建立极坐标系, 已知点
轴的非负半轴为极轴建立极坐标系, 已知点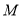 的极坐标为
的极坐标为 ,曲线
,曲线 的参数方程为
的参数方程为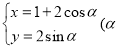 为参数).
为参数).(1)直线
 过
过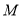 且与曲线
且与曲线 相切, 求直线
相切, 求直线 的极坐标方程;
的极坐标方程;(2)点
 与点
与点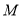 关于
关于 轴对称, 求曲线
轴对称, 求曲线 上的点到点
上的点到点 的距离的取值范围.
的距离的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某烟花厂家为了测试最新研制出的一种“冲天”产品升空的安全性,特对其进行了一项测试。如图,这种烟花在燃放点C进行燃放实验,测试人员甲、乙分别在A,B两地(假设三地在同一水平面上),测试人员甲测得A、B两地相距80米且∠BAC=60°,甲听到烟花燃放“冲天”时的声音的时间比乙晚
 秒.在A地测得该烟花升至最高点H处的仰角为60°.(已知声音的传播速度为340米∕秒)
秒.在A地测得该烟花升至最高点H处的仰角为60°.(已知声音的传播速度为340米∕秒)(1)求甲距燃放点C的距离;(2)求这种烟花的垂直“冲天”高度HC

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A. 空间不同的三点确定一个平面
B. 空间两两相交的三条直线确定一个平面
C. 空间有三个角为直角的四边形一定是平面图形
D. 和同一条直线相交的三条平行直线一定在同一平面内
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

 ,
,(1)若曲线
 在点
在点 处的切线为
处的切线为 ,求
,求 的值;
的值;(2)讨论函数
 的单调性;
的单调性;(3)设函数
 ,若至少存在一个
,若至少存在一个 ,使得
,使得 成立,求实数
成立,求实数 的取值范.
的取值范. -
科目: 来源: 题型:
查看答案和解析>>【题目】下表提供了某公司技术升级后生产
 产品过程中记录的产量
产品过程中记录的产量 (吨)与相应的成本
(吨)与相应的成本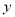 (万元)的几组对照数据:
(万元)的几组对照数据:
(1)请画出上表数据的散点图;

(2)请根据上表提供的数据,用最小二乘法求出
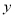 对
对 的回归直线方程;
的回归直线方程;(3)已知该公司技术升级前生产100吨
 产品的成本为90万元.试根据(2)求出的回归直线方程,预测技术升级后生产100吨
产品的成本为90万元.试根据(2)求出的回归直线方程,预测技术升级后生产100吨 产品的成本比技术升级前约降低多少万元?
产品的成本比技术升级前约降低多少万元?(附:
 ,
,  ,其中
,其中 为样本平均值)
为样本平均值)
相关试题

