【题目】某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对![]() 名出租车司机进行调查,调查问卷共
名出租车司机进行调查,调查问卷共![]() 道题,答题情况如下表:
道题,答题情况如下表:
答对题目数 |
|
|
|
|
女 |
|
|
|
|
男 |
|
|
|
|
(I)如果出租车司机答对题目大于等于![]() ,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;
,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;
(II)从答对题目数小于![]() 的出租车司机中选出
的出租车司机中选出![]() 人做进一步的调查,求选出的
人做进一步的调查,求选出的![]() 人中至少有一名女出租车司机的概率.
人中至少有一名女出租车司机的概率.
参考答案:
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】
试题分析:(I)求出出租车司机答对题目数大于等于![]() 的人数,代入古典概型概率计算公式,可得答案;(2)求出从答对题目数少于
的人数,代入古典概型概率计算公式,可得答案;(2)求出从答对题目数少于![]() 的出租车司机中任选出两人的情况总数和选出的两人中至少有一名女出租车司机的情况个数,代入古典概型概率计算公式,可得答案.
的出租车司机中任选出两人的情况总数和选出的两人中至少有一名女出租车司机的情况个数,代入古典概型概率计算公式,可得答案.
试题解析:(I)答对题目数小于![]() 的人数为
的人数为![]() ,记“答对题目数大于等于
,记“答对题目数大于等于![]() ”为事件
”为事件![]() ,
,
![]() . …………………(6分)
. …………………(6分)
(II)设答对题目数小于![]() 的司机为
的司机为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() 为女司机,任选出
为女司机,任选出![]() 人包含
人包含![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,共
,共![]() 种,至少有一名女出租车司机的事件为
种,至少有一名女出租车司机的事件为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共
,共![]() 种,记“选出的
种,记“选出的![]() 人中至少有一名女出租车司机”为事件
人中至少有一名女出租车司机”为事件![]() ,则
,则![]() .…………………(12分)
.…………………(12分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
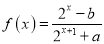 是
是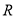 的奇函数,
的奇函数, 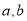 是常数.
是常数.(1)求
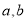 的值;
的值;(2)用定义法证明
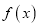 是
是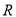 的增函数;
的增函数;(3)不等式
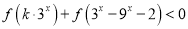 对任意
对任意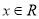 恒成立,求实数
恒成立,求实数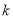 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】设
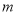 是实数,
是实数,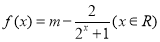 ,
,(1)若函数
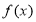 为奇函数,求
为奇函数,求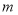 的值;
的值;(2)试用定义证明:对于任意
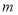 ,
,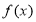 在
在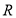 上为单调递增函数;
上为单调递增函数;(3)若函数
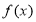 为奇函数,且不等式
为奇函数,且不等式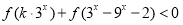 对任意
对任意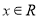 恒成立,求实数
恒成立,求实数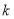 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某车间20名工人年龄数据如下表:
年龄(岁)
19
24
26
30
34
35
40
合计
工人数(人)
1
3
3
5
4
3
1
20
(1)求这20名工人年龄的众数与平均数;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】心理学家分析发现“喜欢空间想象”与“性别”有关,某数学兴趣小组为了验证此结论,从全体组员中按分层抽样的方法抽取50名同学(男生30人、女生20人),给每位同学立体几何题、代数题各一道,让各位同学自由选择一道题进行解答,选题情况统计如下表:(单位:人)
立体几何题
代数题
总计
男同学
22
8
30
女同学
8
12
20
总计
30
20
50
(1)能否有97.5%以上的把握认为“喜欢空间想象”与“性别”有关?
(2)经统计得,选择做立体几何题的学生正答率为
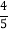 ,且答对的学生中男生人数是女生人数的5倍,现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究,求恰好抽到男女生各一人的概率.
,且答对的学生中男生人数是女生人数的5倍,现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究,求恰好抽到男女生各一人的概率.附表及公式:
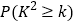
0.15
0.10
0.05
0.025
0.010
0.005
0.001
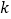
2.072
2.706
3.841
5.024
6.635
7.879
10.828
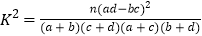
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
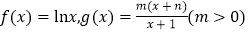 .
.(1)当
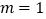 时,函数
时,函数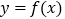 与
与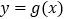 在
在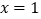 处的切线互相垂直,求
处的切线互相垂直,求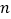 的值;
的值;(2)若函数
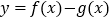 在定义域内不单调,求
在定义域内不单调,求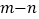 的取值范围;
的取值范围;(3)是否存在正实数
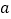 ,使得
,使得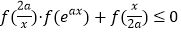 对任意正实数
对任意正实数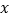 恒成立?若存在,求出满足条件的实数
恒成立?若存在,求出满足条件的实数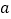 ;若不存在,请说明理由.
;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知p:指数函数f(x)=(2a-6)x在R上是单调减函数;q:关于x的方程x2-3ax+2a2+1=0的两根均大于3,若p或q为真,p且q为假,求实数a的取值范围.
相关试题

