
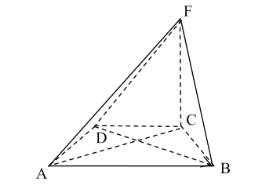
【题目】在如图所示的四棱锥![]() 中,四边形
中,四边形![]() 是等腰梯形,
是等腰梯形,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)已知二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由已知可得![]() ,结合
,结合![]() ,由直线与平面垂直的判定可得
,由直线与平面垂直的判定可得![]() 平面
平面![]() ;
;
(2)由(1)知,![]() ,则
,则![]() ,
,![]() ,
,![]() 两两互相垂直,以
两两互相垂直,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,设
轴建立空间直角坐标系,设![]() ,0,
,0,![]() ,由二面角
,由二面角![]() 的余弦值为
的余弦值为![]() 求解
求解![]() ,再由空间向量求解直线
,再由空间向量求解直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)证明:因为四边形![]() 是等腰梯形,
是等腰梯形,![]() ,
,![]() ,所以
,所以![]() .又
.又![]() ,所以
,所以![]() ,
,
因此![]() ,
,![]() ,
,
又![]() ,
,
且![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
由于![]() ,因此
,因此![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .
.
由于![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,故
,故![]() ,
,
所以![]() 为二面角
为二面角![]() 的平面角.在等腰三角形
的平面角.在等腰三角形![]() 中,由于
中,由于![]() ,
,
因此![]() ,又
,又![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]()
以![]() 为
为![]() 轴、
轴、![]() 为
为![]() 轴、
轴、![]() 为
为![]() 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则![]() ,
,![]() ,
,![]()
 ,
, ,
,
设平面![]() 的法向量为
的法向量为![]()
所以 ,即
,即 ,令
,令![]() ,则
,则![]() ,
,![]() ,
,
则平面![]() 的法向量
的法向量![]() ,
,![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]()



 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,如图4①,②,③,④为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.

(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭记录了未使用节水龙头30天的日用水量数据(单位:![]() )和使用了节水龙头30天的日用水量数据,得到频数分布表如下:
)和使用了节水龙头30天的日用水量数据,得到频数分布表如下:
(一)未使用节水龙头30天的日用水量频数分布表
日用水量 |
|
|
|
|
|
频数 | 2 | 3 | 8 | 12 | 5 |
(二)使用了节水龙头30天的日用水量频数分布表
日用水量 |
|
|
|
|
|
频数 | 2 | 5 | 11 | 6 | 6 |
(1)估计该家庭使用了节水龙头后,日用水量小于![]() 的概率;
的概率;
(2)估计该家庭使用节水龙头后,平均每天能节省多少水?(同一组中的数据以这组数据所在区间中点的值作代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知若椭圆![]() :
:![]() (
(![]() )交
)交![]() 轴于
轴于![]() ,
,![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
,![]() 的任意一点,直线
的任意一点,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() ,则
,则![]() 为定值
为定值![]() .
.
(1)若将双曲线与椭圆类比,试写出类比得到的命题;
(2)判定(1)类比得到命题的真假,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() :
:![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,
,![]() ,离心率为
,离心率为![]() ,左、右顶点分别为
,左、右顶点分别为![]() ,
,![]() .过
.过![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的线段长为1.
截得的线段长为1.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)经过点![]() 的直线与椭圆
的直线与椭圆![]() 相交于不同的两点
相交于不同的两点![]() 、
、![]() (不与点
(不与点![]() 、
、![]() 重合),直线
重合),直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,求证:
,求证:![]() 、
、![]() 、
、![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S- ABCD中,SD⊥底面ABCD,AB//DC,AD ⊥ DC,,AB=AD=1DC=SD=2, E为棱SB上的一点,且SE=2EB.
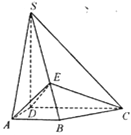
(I)证明:DE⊥平面SBC;
(II)证明:求二面角A- DE -C的大小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的两个零点之差的绝对值的最小值为
的两个零点之差的绝对值的最小值为![]() ,将函数
,将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度得到函数
个单位长度得到函数![]() 的图象,则下列说法正确的是( )
的图象,则下列说法正确的是( )
①函数![]() 的最小正周期为
的最小正周期为![]() ;②函数
;②函数![]() 的图象关于点(
的图象关于点(![]() )对称;
)对称;
③函数![]() 的图象关于直线
的图象关于直线![]() 对称;④函数
对称;④函数![]() 在
在![]() 上单调递增.
上单调递增.
A.①②③④B.①②C.②③④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是以
是以![]() 为直径的半圆上异于点
为直径的半圆上异于点![]() 的点,矩形
的点,矩形![]() 所在的平面垂直于该半圆所在平面,且
所在的平面垂直于该半圆所在平面,且![]()
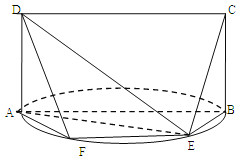
(Ⅰ)求证:![]() ;
;
(Ⅱ)设平面![]() 与半圆弧的另一个交点为
与半圆弧的另一个交点为![]() ,
,
①求证:![]() //
//![]() ;
;
②若![]() ,求三棱锥E-ADF的体积.
,求三棱锥E-ADF的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com