【题目】已知若椭圆：（）交轴于，两点，点是椭圆上异于，的任意一点，直线，分别交轴于点，，则为定值.

（1）若将双曲线与椭圆类比，试写出类比得到的命题；

（2）判定（1）类比得到命题的真假，请说明理由.

【答案】（1）见解析；（2）命题为真命题，证明见解析.

【解析】

（1）根据类比推理的基本原则可直接写出结果；

（2）设，，，表示出直线方程后可求得点坐标，由此得到，同理得到，根据平面向量的数量积运算可构造方程，结合点在双曲线上可化简得到结果.

（1）类比得命题：若双曲线：交轴于两点，点是双曲线上异于的任意一点，直线分别交轴于点，则为定值.

（2）在（1）中类比得到的命题为真命题，证明如下：

不妨设，，，则，

∴直线方程为.

令，则，∴点坐标为.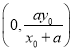

又，∴.

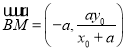同法可求得：.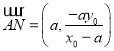

∴.

又∵，∴.

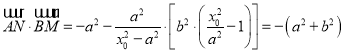关闭