【题目】如图，四棱锥S- ABCD中，SD⊥底面ABCD，AB//DC，AD ⊥ DC,，AB=AD＝1DC=SD=2， E为棱SB上的一点，且SE=2EB．

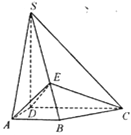
(I)证明：DE⊥平面SBC；

(II)证明：求二面角A- DE -C的大小

【答案】（Ⅰ）证明略；(Ⅱ)．

【解析】

试题（Ⅰ）先根据题意建立适当的空间直角坐标系，写出相关点的坐标，利用空间向量证明线线垂直，再利用线面垂直的判定定理进行证明；(Ⅱ)求出两平面的法向量，求出法向量的夹角，再结合图形确定二面角的大小.

试题解析：分别以，，所在直线为x轴，轴，z建立空间直角坐标系（如图），

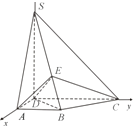
则，

（Ⅰ）∵SE=2EB，

∴

又

∴

∴

又∴DE平面SBC

(Ⅱ) 由(Ⅰ)知，DE⊥平面SBC，

∵平面SBC，∴

当时，知，，

取中点，则，

故，由此得FA⊥DE

∴向量与的夹角等于二面角的平面角

又，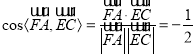

∴二面角的大小为

关闭