
【题目】椭圆![]() :
:![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,
,![]() ,离心率为
,离心率为![]() ,左、右顶点分别为
,左、右顶点分别为![]() ,
,![]() .过
.过![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的线段长为1.
截得的线段长为1.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)经过点![]() 的直线与椭圆
的直线与椭圆![]() 相交于不同的两点
相交于不同的两点![]() 、
、![]() (不与点
(不与点![]() 、
、![]() 重合),直线
重合),直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,求证:
,求证:![]() 、
、![]() 、
、![]() 三点共线.
三点共线.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)根据已知可得![]() ,结合离心率和
,结合离心率和![]() 关系,即可求出椭圆
关系,即可求出椭圆![]() 的标准方程;
的标准方程;
(2)![]() 斜率不为零,设
斜率不为零,设![]() 的方程为
的方程为![]() ,与椭圆方程联立,消去
,与椭圆方程联立,消去![]() ,得到
,得到![]() 纵坐标关系,求出
纵坐标关系,求出![]() 方程,令
方程,令![]() 求出
求出![]() 坐标,要证
坐标,要证![]() 、
、![]() 、
、![]() 三点共线,只需证
三点共线,只需证![]() ,将
,将![]() 分子用
分子用![]() 纵坐标表示,即可证明结论.
纵坐标表示,即可证明结论.
(1)由于![]() ,将
,将![]() 代入椭圆方程
代入椭圆方程![]() ,
,
得![]() ,由题意知
,由题意知![]() ,即
,即![]() .
.
又![]() ,所以
,所以![]() ,
,![]() .
.
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)解法一:
依题意直线![]() 斜率不为0,设
斜率不为0,设![]() 的方程为
的方程为![]() ,
,
联立方程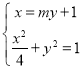 ,消去
,消去![]() 得
得![]() ,
,
由题意,得![]() 恒成立,设
恒成立,设![]() ,
,![]() ,
,
所以![]() ,
,![]()
直线![]() 的方程为
的方程为![]() .令
.令![]() ,得
,得![]() .
.
又因为![]() ,
,![]() ,
,
则直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,
所以![]() .
.
上式中的分子![]()
![]() ,
,
![]() .所以
.所以![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
解法二:
当直线![]() 的斜率
的斜率![]() 不存在时,由题意,得
不存在时,由题意,得![]() 的方程为
的方程为![]() ,
,
代入椭圆![]() 的方程,得
的方程,得![]() ,
,![]() ,
,
直线![]() 的方程为
的方程为![]() .
.
则![]() ,
,![]() ,
,![]() ,
,
所以![]() ,即
,即![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
当直线![]() 的斜率
的斜率![]() 存在时,
存在时,
设![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,
,
联立方程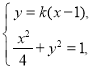 消去
消去![]() ,得
,得![]() .
.
由题意,得![]() 恒成立,故
恒成立,故![]() ,
,![]() .
.
直线![]() 的方程为
的方程为![]() .令
.令![]() ,得
,得![]() .
.
又因为![]() ,
,![]() ,
,
则直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,
所以![]() .
.
上式中的分子![]()
![]()
![]()
![]()
所以![]() .
.
所以![]() ,
,![]() ,
,![]() 三点共线.
三点共线.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的坐标方程为
的坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切.
相切.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() 、
、![]() 于原点
于原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立的极坐标系中,直线
轴的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,点
两点,点![]() 是圆
是圆![]() 上任一点,求
上任一点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 两地相距
两地相距![]() ,某船从
,某船从![]() 地逆水到
地逆水到![]() 地,水速为
地,水速为![]() ,船在静水中的速度为
,船在静水中的速度为![]() .若船每小时的燃料费与其在静水中速度的平方成正比,当
.若船每小时的燃料费与其在静水中速度的平方成正比,当![]() ,每小时的燃料费为
,每小时的燃料费为![]() 元,为了使全程燃料费最省,船的实际速度应为多少?
元,为了使全程燃料费最省,船的实际速度应为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小刘同学大学毕业后自主择业,回到农村老家发展蜜桔收购,然后卖出去,帮助村民致富.小刘打算利用“互联网+”的模式进行销售.为了更好地销售,假设该村每颗蜜柚树结果50个,现随机选了两棵树的蜜柚摘下来进行测重,其质量分布在区间内(单位:千克)的个数:![]() ,10;
,10;![]() ,10;
,10;![]() ,15;
,15;![]() ,40;
,40;![]() ,20;
,20;![]() ,5.
,5.
(1)作出其频率分布直方图并求其众数;
(2)以各组数据的中间数值代表这组数据的平均水平,以频率代表概率,已知该村蜜袖树上大约还有100颗树的蜜柚待出售,小刘提出两种收购方案:

A.所有蜜柚均以16元/千克收购;
B.低于2.25千克的蜜柚以22元/个收购,高于或等于2.25千克的以30元/个收购.请你通过计算为该村选择收益最好的方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com