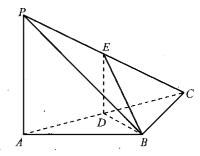
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】试题分析:(Ⅰ)要证明线线垂直,一般转化为证明线面垂直;(Ⅱ)要证明面面垂直,一般转化为证明线面垂直、线线垂直;(Ⅲ)由![]() 即可求解.
即可求解.
试题解析:(I)因为![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(II)因为![]() ,
,![]() 为
为![]() 中点,所以
中点,所以![]() ,
,
由(I)知,![]() ,所以
,所以![]() 平面
平面![]() .
.
所以平面![]() 平面
平面![]() .
.
(III)因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() .
.
因为![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,![]() .
.
由(I)知,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
所以三棱锥![]() 的体积
的体积![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场对某一商品搞活动,已知该商品每一个的进价为3元,销售价为8元,每天售出的第20个及之后的半价出售.该商场统计了近10天的这种商品销量,如图所示:设
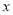 为每天商品的销量,
为每天商品的销量,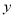 为该商场每天销售这种商品的的利润.从日利润不少于96元的几天里任选2天,则选出的这2天日利润都是97元的概率为( )
为该商场每天销售这种商品的的利润.从日利润不少于96元的几天里任选2天,则选出的这2天日利润都是97元的概率为( )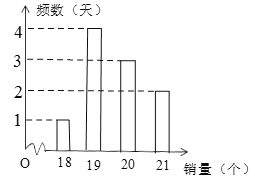
A.
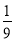 B.
B.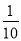 C.
C.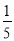 D.
D.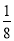
-
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
 :
: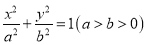 的左顶点为
的左顶点为 ,右焦点为
,右焦点为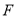 ,上顶点为
,上顶点为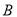 ,下顶点为
,下顶点为 ,若直线
,若直线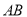 与直线
与直线 的交点为
的交点为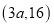 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)点
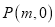 为椭圆
为椭圆 的长轴上的一个动点,过点
的长轴上的一个动点,过点 且斜率为
且斜率为 的直线
的直线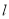 交椭圆
交椭圆 于
于 两点,证明:
两点,证明: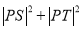 为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】点E、F、G分别是正方体ABCD-A1B1C1D1的棱AB、BC、B1C1的中点,如图所示,则下列命题中的真命题是________(写出所有真命题的编号).
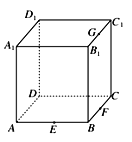
①以正方体的顶点为顶点的三棱锥的四个面中最多只有三个面是直角三角形;
②过点F、D1、G的截面是正方形;
③点P在直线FG上运动时,总有AP⊥DE;
④点Q在直线BC1上运动时,三棱锥A-D1QC的体积是定值;
⑤点M是正方体的平面A1B1C1D1内的到点D和C1距离相等的点,则点M的轨迹是一条线段.
-
科目: 来源: 题型:
查看答案和解析>>【题目】节能减排以来,兰州市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.

(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)估计用电量落在[220,300)中的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且

(1)求证:不论
 为何值,总有平面BEF⊥平面ABC;
为何值,总有平面BEF⊥平面ABC;(2)当λ为何值时,平面BEF⊥平面ACD ?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
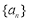 满足:
满足:
(1)求
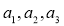 的值;
的值;(2)求证:数列
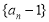 是等比数列;
是等比数列;(3)令
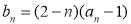 (
(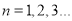 ),如果对任意
),如果对任意 ,都有
,都有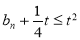 ,求实数
,求实数 的取值范围.
的取值范围.
相关试题

