【题目】节能减排以来,兰州市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图. 
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)估计用电量落在[220,300)中的概率是多少?
参考答案:
【答案】
(1)解:依题意,20×(0.002+0.009 5+0.011+0.012 5+x+0.005+0.002 5)=1,解得x=0.007 5
(2)解:由图可知,最高矩形的数据组为[220,240),
∴众数为 ![]() =230.
=230.
∵[160,220)的频率之和为(0.002+0.009 5+0.011)×20=0.45,
∴依题意,设中位数为y,
∴0.45+(y﹣220)×0.012 5=0.5.解得y=224,∴中位数为224
(3)解:月平均用电量在[220,330)中的概率是p=1﹣(0.002+0.0095+0.011)×20=0.55
【解析】(1)由直方图的性质可得20×(0.002+0.009 5+0.011+0.012 5+x+0.005+0.002 5)=1,解方程可得;(2)由直方图中众数为最高矩形上端的中点可得,可得中位数在[220,240)内,设中位数为a,解方程0.45+(y﹣220)×0.012 5=0.5可得;(3)月平均用电量在[220,330)中的概率是p=1﹣(0.002+0.0095+0.011)×20.
【考点精析】根据题目的已知条件,利用频率分布直方图的相关知识可以得到问题的答案,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.
-
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
 :
: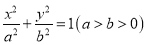 的左顶点为
的左顶点为 ,右焦点为
,右焦点为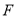 ,上顶点为
,上顶点为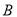 ,下顶点为
,下顶点为 ,若直线
,若直线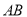 与直线
与直线 的交点为
的交点为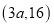 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)点
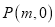 为椭圆
为椭圆 的长轴上的一个动点,过点
的长轴上的一个动点,过点 且斜率为
且斜率为 的直线
的直线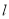 交椭圆
交椭圆 于
于 两点,证明:
两点,证明: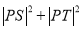 为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】点E、F、G分别是正方体ABCD-A1B1C1D1的棱AB、BC、B1C1的中点,如图所示,则下列命题中的真命题是________(写出所有真命题的编号).
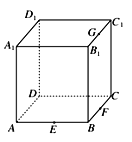
①以正方体的顶点为顶点的三棱锥的四个面中最多只有三个面是直角三角形;
②过点F、D1、G的截面是正方形;
③点P在直线FG上运动时,总有AP⊥DE;
④点Q在直线BC1上运动时,三棱锥A-D1QC的体积是定值;
⑤点M是正方体的平面A1B1C1D1内的到点D和C1距离相等的点,则点M的轨迹是一条线段.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且

(1)求证:不论
 为何值,总有平面BEF⊥平面ABC;
为何值,总有平面BEF⊥平面ABC;(2)当λ为何值时,平面BEF⊥平面ACD ?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
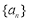 满足:
满足:
(1)求
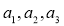 的值;
的值;(2)求证:数列
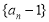 是等比数列;
是等比数列;(3)令
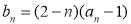 (
(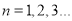 ),如果对任意
),如果对任意 ,都有
,都有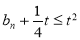 ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格纸上小正方形的边长为
 ,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
A.
 B.
B.  C.
C.  D.
D. 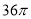
相关试题

