【题目】已知数列![]() 满足:
满足:![]()
(1)求![]() 的值;
的值;
(2)求证:数列![]() 是等比数列;
是等比数列;
(3)令![]() (
(![]() ),如果对任意
),如果对任意![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 是以
是以![]() 为首相
为首相![]() 为公比的等比数列;
为公比的等比数列;
(3)![]()
【解析】
试题分析:(1)利用赋值法,令![]() 可求
可求![]() ;
;
(2)将等式写到![]() ,再将得到的式子与已知等式联立,两式再相减,根据等比数列的定
,再将得到的式子与已知等式联立,两式再相减,根据等比数列的定![]() ,可证明
,可证明![]() 是以
是以![]() 为首相
为首相![]() 为公比的等比数列;
为公比的等比数列;
(3)由(2)可写出![]() ,利用数列的单调性当
,利用数列的单调性当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,因此,数列
,因此,数列![]() 的最大值为
的最大值为![]() ,则
,则![]() 可解的
可解的![]() 的范围.
的范围.
试题解析:(1)![]()
(2)由题可知:![]() ①
①
![]() ②
②
②-①可得![]() 即:
即:![]() ,又
,又![]()
∴数列![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列
为公比的等比数列
(3)由(2)可得![]() ,
, ![]()
由![]() 可得
可得![]()
由![]() 可得
可得![]() ,所以
,所以 ![]()
故![]() 有最大值
有最大值![]()
所以,对任意![]() ,有
,有![]()
如果对任意![]() ,都有
,都有![]() ,即
,即![]() 成立,
成立,
则![]() ,故有:
,故有:![]() ,解得
,解得![]() 或
或![]()
∴实数![]() 的取值范围是
的取值范围是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】节能减排以来,兰州市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.

(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)估计用电量落在[220,300)中的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且

(1)求证:不论
 为何值,总有平面BEF⊥平面ABC;
为何值,总有平面BEF⊥平面ABC;(2)当λ为何值时,平面BEF⊥平面ACD ?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格纸上小正方形的边长为
 ,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
A.
 B.
B.  C.
C.  D.
D. 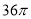
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线
 的极坐标方程是
的极坐标方程是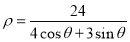 ,以极点为原点
,以极点为原点 ,极轴为
,极轴为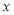 轴正半轴(两坐标系取相同的单位长度)的直角坐标系
轴正半轴(两坐标系取相同的单位长度)的直角坐标系 中,曲线
中,曲线 的参数方程为:
的参数方程为: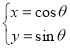 (
(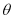 为参数).
为参数).(1)求曲线
 的直角坐标方程与曲线
的直角坐标方程与曲线 的普通方程;
的普通方程;(2)若用
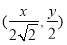 代换曲线
代换曲线 的普通方程中的
的普通方程中的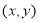 得到曲线
得到曲线 的方程,若
的方程,若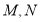 分别是曲线
分别是曲线 和曲线
和曲线 上的动点,求
上的动点,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着手机使用的不断普及,现在全国各地的中小学生携带手机进入校园已经成为了普遍的现象,也引起了一系列的问题。然而,是堵还是疏,就摆在了我们学校老师的面前.某研究型学习小组调查研究“中学生使用手机对学习的影响”,部分统计数据如下表:
不使用手机
使用手机
合计
学习成绩优秀人数
18
7
25
学习成绩不优秀人数
6
19
25
合计
24
26
50
参考数据:
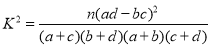 ,其中
,其中 .
.
0.10
0.05
0.025
0.010
0.005
0.001
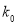
2.706
3.841
5.024
6.635
7.879
10.828
(1)试根据以上数据,运用独立性检验思想,指出有多大把握认为中学生使用手机对学习有影响?
(2)研究小组将该样本中使用手机且成绩优秀的7位同学记为
 组,不使用手机且成绩优秀的18位同学记为
组,不使用手机且成绩优秀的18位同学记为 组,计划从
组,计划从 组推选的2人和
组推选的2人和 组推选的3人中,随机挑选两人来分享学习经验.求挑选的两人中一人来自
组推选的3人中,随机挑选两人来分享学习经验.求挑选的两人中一人来自 组、另一人来自
组、另一人来自 组的概率.
组的概率.
相关试题

