搜索
【题目】若函数f（x）=loga（x+ 
）是奇函数，则a= ．
参考答案：
【答案】
【解析】解：∵函数 
是奇函数，
∴f（x）+f（﹣x）=0
即loga（x+ 
）+loga（﹣x+ ）=0
∴loga（x+ ）×（﹣x+ ）=0
∴x2+2a2﹣x2=1，即2a2=1，
∴a=±
又a对数式的底数，a＞0
∴a=
故应填
【考点精析】利用函数奇偶性的性质和对数的运算性质对题目进行判断即可得到答案，需要熟知在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇；①加法：
②减法：
③数乘：
④
⑤
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四棱锥P－ABCD中，AD⊥平面PAB，AP⊥AB．
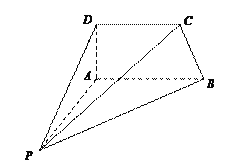
（1）求证：CD⊥AP；
（2）若CD⊥PD，求证：CD∥平面PAB；
-
科目： 来源： 题型：
查看答案和解析>>【题目】设P和0是两个集合，定义集合PQ={x|x∈P，且x≠Q}，如果P={x|log2x＜1}，Q={x||x﹣2|＜1}，那么PQ等于 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】【选做题】在A、B、C、D四小题中只能选做2题，每小题10分，共计20分．请在答卷卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．
A．选修4—1：几何证明选讲
如图，△ABC的顶点A，C在圆O上，B在圆外，线段AB与圆O交于点M．
（1）若BC是圆O的切线，且AB＝8，BC＝4，求线段AM的长度；
（2）若线段BC与圆O交于另一点N，且AB＝2AC，求证：BN＝2MN．
B．选修4—2：矩阵与变换
设a，b∈R．若直线l：ax＋y－7＝0在矩阵A=
对应的变换作用下，得到的直线为l′：9x＋y－91＝0．求实数a，b的值．C．选修4—4：坐标系与参数方程
在平面直角坐标系xOy中，直线l：
(t为参数)，与曲线C： 
(k为参数)交于A，B两点，求线段AB的长．D．选修4—5：不等式选讲
设a≠b，求证：a4＋6a2b2＋b4＞4ab(a2＋b2)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两位小学生各有2008年奥运吉祥物“福娃”5个（其中“贝贝”、“晶晶”、“欢欢”、“迎迎”和“妮妮各一个”），现以投掷一个骰子的方式进行游戏，规则如下：当出现向上的点数是奇数时，甲赢得乙一个福娃；否则乙赢得甲一个福娃，规定掷骰子的次数达9次时，或在此前某人已赢得所有福娃时游戏终止．记游戏终止时投掷骰子的次数为ξ
（1）求掷骰子的次数为7的概率；
（2）求ξ的分布列及数学期望Eξ． -
科目： 来源： 题型：
查看答案和解析>>【题目】一家公司计划生产某种小型产品的月固定成本为1万元，每生产1万件需要再投入2万元，设该公司一个月内生产该小型产品x万件并全部销售完，每万件的销售收入为4﹣x万元，且每万件国家给予补助2e﹣
﹣ 
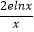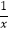万元．（e为自然对数的底数，e是一个常数）
（1）写出月利润f（x）（万元）关于月产量x（万件）的函数解析式
（2）当月产量在[1，2e]万件时，求该公司在生产这种小型产品中所获得的月利润最大值（万元）及此时的月生成量值（万件）．（注：月利润=月销售收入+月国家补助﹣月总成本） -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
．
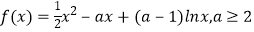（1）求函数f（x）的单调区间；
（2）证明：若a＜5，则对任意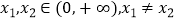
，有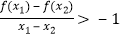 
．
相关试题
