【题目】【选做题】在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答卷卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.
A.选修4—1:几何证明选讲
如图,△ABC的顶点A,C在圆O上,B在圆外,线段AB与圆O交于点M.

(1)若BC是圆O的切线,且AB=8,BC=4,求线段AM的长度;
(2)若线段BC与圆O交于另一点N,且AB=2AC,求证:BN=2MN.
B.选修4—2:矩阵与变换
设a,b∈R.若直线l:ax+y-7=0在矩阵A= ![]() 对应的变换作用下,得到的直线为l′:9x+y-91=0.求实数a,b的值.
对应的变换作用下,得到的直线为l′:9x+y-91=0.求实数a,b的值.
C.选修4—4:坐标系与参数方程
在平面直角坐标系xOy中,直线l:  (t为参数),与曲线C:
(t为参数),与曲线C:  (k为参数)交于A,B两点,求线段AB的长.
(k为参数)交于A,B两点,求线段AB的长.
D.选修4—5:不等式选讲
设a≠b,求证:a4+6a2b2+b4>4ab(a2+b2).
参考答案:
【答案】见解析.
试题分析:作差比较,化简得出原式=![]() ,即可作出证明。
,即可作出证明。
试题解析:
证明: a4+6a2b2+b4-4ab(a2+b2)=(a2+b2)2-4ab(a2+b2)+4a2b2
=(a2+b2-2ab)2=(a-b)4.
因为a≠b,所以(a-b)4>0, 所以a4+6a2b2+b4>4ab(a2+b2).
【解析】试题分析:(1)因为![]() 是圆
是圆![]() 的切线,故由切割线定理得
的切线,故由切割线定理得![]() ,设
,设![]() ,列出方程,即可求解
,列出方程,即可求解![]() 的值,得到
的值,得到![]() 的长;
的长;
(2)根据![]() 和
和![]() 相似,列出比例关系式,即可得出证明。
相似,列出比例关系式,即可得出证明。
试题解析:
解:(1)因为BC是圆O的切线,故由切割线定理得BC2=BM·BA.
设AM=t,因为AB=8,BC=4,
所以42=8(8-t),解得t=6 ,即线段AM的长度为6.
(2)因为四边形AMNC为圆内接四边形,所以∠A=∠MNB.又∠B=∠B,所以△BMN∽△BCA,
所以![]() =
=![]() .
.
因为AB=2AC,所以BN=2MN.
B.选修4—2:矩阵与变换
设a,b∈R.若直线l:ax+y-7=0在矩阵A= ![]() 对应的变换作用下,得到的直线为l′:9x+y-91=0.求实数a,b的值.
对应的变换作用下,得到的直线为l′:9x+y-91=0.求实数a,b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,则甲、乙两名运动员的中位数分别为( )
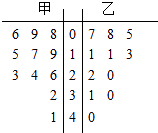
A.19、13
B.13、19
C.20、18
D.18、20 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P-ABCD中,AD⊥平面PAB,AP⊥AB.
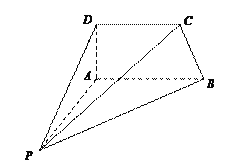
(1)求证:CD⊥AP;
(2)若CD⊥PD,求证:CD∥平面PAB;
-
科目: 来源: 题型:
查看答案和解析>>【题目】设P和0是两个集合,定义集合PQ={x|x∈P,且x≠Q},如果P={x|log2x<1},Q={x||x﹣2|<1},那么PQ等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)=loga(x+
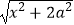 )是奇函数,则a= .
)是奇函数,则a= . -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位小学生各有2008年奥运吉祥物“福娃”5个(其中“贝贝”、“晶晶”、“欢欢”、“迎迎”和“妮妮各一个”),现以投掷一个骰子的方式进行游戏,规则如下:当出现向上的点数是奇数时,甲赢得乙一个福娃;否则乙赢得甲一个福娃,规定掷骰子的次数达9次时,或在此前某人已赢得所有福娃时游戏终止.记游戏终止时投掷骰子的次数为ξ
(1)求掷骰子的次数为7的概率;
(2)求ξ的分布列及数学期望Eξ. -
科目: 来源: 题型:
查看答案和解析>>【题目】一家公司计划生产某种小型产品的月固定成本为1万元,每生产1万件需要再投入2万元,设该公司一个月内生产该小型产品x万件并全部销售完,每万件的销售收入为4﹣x万元,且每万件国家给予补助2e﹣
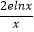 ﹣
﹣ 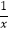 万元.(e为自然对数的底数,e是一个常数)
万元.(e为自然对数的底数,e是一个常数)
(1)写出月利润f(x)(万元)关于月产量x(万件)的函数解析式
(2)当月产量在[1,2e]万件时,求该公司在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生成量值(万件).(注:月利润=月销售收入+月国家补助﹣月总成本)
相关试题

