【题目】已知函数![]() ,
, ![]() 为实常数.
为实常数.
(Ⅰ)设![]() ,当
,当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,直线
时,直线![]() 、
、![]() 与函数
与函数![]() 、
、![]() 的图象一共有四个不同的交点,且以此四点为顶点的四边形恰为平行四边形.
的图象一共有四个不同的交点,且以此四点为顶点的四边形恰为平行四边形.
求证: ![]() .
.
参考答案:
【答案】(1)单调递增区间为![]() ,无单调递减区间;(2)证明见解析.
,无单调递减区间;(2)证明见解析.
【解析】试题分析:(Ⅰ)求函数的导数![]() ,因为
,因为![]() ,所以显然
,所以显然![]() 得到函数的单调区间;(Ⅱ)一组对边平行且相等的四边形为平行四边形,即
得到函数的单调区间;(Ⅱ)一组对边平行且相等的四边形为平行四边形,即![]() ,所以分析函数
,所以分析函数![]() ,根据函数的二阶导数可判断函数在
,根据函数的二阶导数可判断函数在![]() 为减函数,在
为减函数,在![]() 为增函数,若
为增函数,若![]() ,即一个根小于1,一个根大于1,即得结果.
,即一个根小于1,一个根大于1,即得结果.
试题解析:(Ⅰ) ![]() ,其定义域为
,其定义域为![]()
而![]() ,
,
当![]() 时,
时, ![]() ,
,
故F(x)的单调递增区间为![]() ,无单调递减区间.
,无单调递减区间.
(Ⅱ)因为直线![]() 与
与![]() 平行,
平行,
故该四边形为平行四边形等价于![]() 且
且![]() .
.
当![]() 时,
时, ![]() ,
,
则![]() .令
.令![]()
则 ![]() ,
,
故![]() 在
在![]() 上单调递增;
上单调递增;
而![]() ,
,
故![]() 时
时![]() 单调递减;
单调递减; ![]() 时
时![]() 单调递增;
单调递增;
而![]() ,
,
故![]() 或0 < n <1< m,
或0 < n <1< m,
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}中,a1=8,a4=2,且满足an+2﹣2an+1+an=0,n∈N* .
(1)求数列{an}的通项;
(2)设Sn=|a1|+|a2|+…+|an|,求Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】2015年12月,华中地区数城市空气污染指数“爆表”,此轮污染为2015年以来最严重的污染过程,为了探究车流量与
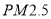 的浓度是否相关,现采集到华中某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市2015年12月份某星期星期一到星期日某一时间段车流量与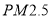 的数据如表:
的数据如表:时间
星期一
星期二
星期三
星期四
星期五
星期六
星期日
车流量
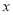 (万辆)
(万辆)1
2
3
4
5
6
7
 的浓度
的浓度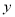 (微克/立方米)
(微克/立方米)28
30
35
41
49
56
62
(1)由散点图知
 与
与 具有线性相关关系,求
具有线性相关关系,求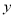 关于
关于 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: 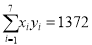 )
)(2)(I)利用(1)所求的回归方程,预测该市车流量为12万辆时
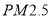 的浓度;(II)规定:当一天内
的浓度;(II)规定:当一天内 的浓度平均值在
的浓度平均值在 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内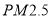 的浓度平均值在
的浓度平均值在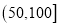 内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量不超过多少万辆?(结果以万辆为单位,保留整数)参考公式:回归直线的方程是
内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量不超过多少万辆?(结果以万辆为单位,保留整数)参考公式:回归直线的方程是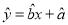 ,其中
,其中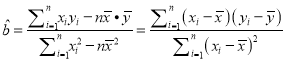 ,
,  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1 .
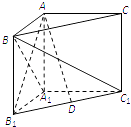
(1)求证:AB1⊥平面A1BC1;
(2)若D为B1C1的中点,求AD与平面A1BC1所成的角. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到如下列联表(平均每天喝500ml以上为常喝,体重超过50kg为肥胖):
常喝
不常喝
合计
肥胖
2
不肥胖
18
合计
30
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为
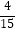 .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)现从常喝碳酸饮料且肥胖的学生中(2名女生),抽取2人参加电视节目,则正好抽到一男一女的概率是多少P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
K
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:K2=
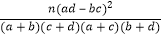 ,其中n=a+b+c+d)
,其中n=a+b+c+d) -
科目: 来源: 题型:
查看答案和解析>>【题目】给定椭圆C:
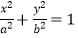 (a>b>0).称圆心在原点O,半径为
(a>b>0).称圆心在原点O,半径为 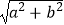 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F( 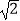 ,0),其短轴上的一个端点到点F的距离为
,0),其短轴上的一个端点到点F的距离为 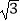 .
.
(1)求椭圆C的方程和其“准圆”方程;
(2)点P是椭圆C的“准圆”上的一个动点,过动点P作直线l1 , l2 , 使得l1 , l2与椭圆C都只有一个交点,试判断l1 , l2是否垂直,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知过
 的动圆恒与
的动圆恒与 轴相切,设切点为
轴相切,设切点为 是该圆的直径.
是该圆的直径.(Ⅰ)求
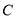 点轨迹
点轨迹 的方程;
的方程;(Ⅱ)当
 不在y轴上时,设直线
不在y轴上时,设直线 与曲线
与曲线 交于另一点
交于另一点 ,该曲线在
,该曲线在 处的切线与直线
处的切线与直线 交于
交于 点.求证:
点.求证:  恒为直角三角形.
恒为直角三角形.
相关试题

