【题目】给定椭圆C: ![]() (a>b>0).称圆心在原点O,半径为
(a>b>0).称圆心在原点O,半径为 ![]() 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F( ![]() ,0),其短轴上的一个端点到点F的距离为
,0),其短轴上的一个端点到点F的距离为 ![]() .
.
(1)求椭圆C的方程和其“准圆”方程;
(2)点P是椭圆C的“准圆”上的一个动点,过动点P作直线l1 , l2 , 使得l1 , l2与椭圆C都只有一个交点,试判断l1 , l2是否垂直,并说明理由.
参考答案:
【答案】
(1)解:由题意可得,c= ![]() ,
, ![]() =a=
=a= ![]() ,
,
则b2=a2﹣c2=1,
则椭圆C的方程为 ![]() +y2=1.
+y2=1.
其“准圆”方程为x2+y2=4
(2)解:①设P(± ![]() ,±1),则过P的直线l1:x=±
,±1),则过P的直线l1:x=± ![]() ,
,
则l2的斜率k≠0,即它们不垂直;
②设P(m,n)(m≠± ![]() ),m2+n2=4,过P的直线为y﹣n=k(x﹣m),
),m2+n2=4,过P的直线为y﹣n=k(x﹣m),
联立椭圆方程,消去y,得到
(1+3k2)x2+6k(n﹣km)x+3(n﹣km)2﹣3=0,
由于直线与椭圆C都只有一个交点,则△=0,
即36k2(n﹣km)2﹣4(1+3k2)3[(n﹣km)2﹣1]=0,
化简得,(3﹣m2)k2+2kmn+1﹣n2=0,
k1k2= ![]() =
= ![]() =﹣1.
=﹣1.
即l1,l2垂直.
综上,当P在直线x= ![]() 上时,l1,l2不垂直;
上时,l1,l2不垂直;
当P不在直线x= ![]() 上时,l1,l2垂直
上时,l1,l2垂直
【解析】(1)由题意可得,c= ![]() ,a=
,a= ![]() ,则b2=a2﹣c2=1,从而得到椭圆方程和其“准圆”方程;(2)讨论当P在直线x=
,则b2=a2﹣c2=1,从而得到椭圆方程和其“准圆”方程;(2)讨论当P在直线x= ![]() 上时,显然不垂直;当P不在直线x=
上时,显然不垂直;当P不在直线x= ![]() 上时,设出直线方程,联立椭圆方程,消去y,得到关于x的方程,运用判别式为0,化简整理,得到关于k的方程,求出两根之积,判断是否为﹣1,即可判断
上时,设出直线方程,联立椭圆方程,消去y,得到关于x的方程,运用判别式为0,化简整理,得到关于k的方程,求出两根之积,判断是否为﹣1,即可判断
l1 , l2垂直.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1 .
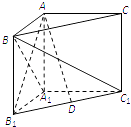
(1)求证:AB1⊥平面A1BC1;
(2)若D为B1C1的中点,求AD与平面A1BC1所成的角. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  为实常数.
为实常数.(Ⅰ)设
 ,当
,当 时,求函数
时,求函数 的单调区间;
的单调区间;(Ⅱ)当
 时,直线
时,直线 、
、 与函数
与函数 、
、 的图象一共有四个不同的交点,且以此四点为顶点的四边形恰为平行四边形.
的图象一共有四个不同的交点,且以此四点为顶点的四边形恰为平行四边形.求证:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到如下列联表(平均每天喝500ml以上为常喝,体重超过50kg为肥胖):
常喝
不常喝
合计
肥胖
2
不肥胖
18
合计
30
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为
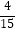 .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)现从常喝碳酸饮料且肥胖的学生中(2名女生),抽取2人参加电视节目,则正好抽到一男一女的概率是多少P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
K
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:K2=
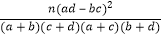 ,其中n=a+b+c+d)
,其中n=a+b+c+d) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知过
 的动圆恒与
的动圆恒与 轴相切,设切点为
轴相切,设切点为 是该圆的直径.
是该圆的直径.(Ⅰ)求
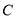 点轨迹
点轨迹 的方程;
的方程;(Ⅱ)当
 不在y轴上时,设直线
不在y轴上时,设直线 与曲线
与曲线 交于另一点
交于另一点 ,该曲线在
,该曲线在 处的切线与直线
处的切线与直线 交于
交于 点.求证:
点.求证:  恒为直角三角形.
恒为直角三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某研究型学习小组调查研究”中学生使用智能手机对学习的影响”.部分统计数据如下表:
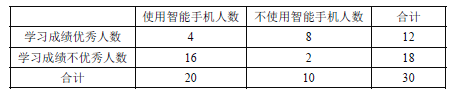
参考数据:

参考公式:
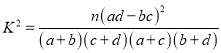 ,其中
,其中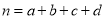
(Ⅰ)试根据以上数据,运用独立性检验思想,指出有多大把握认为中学生使用智能手机对学习有影响?
(Ⅱ)研究小组将该样本中使用智能手机且成绩优秀的4位同学记为
 组,不使用智能手机且成绩优秀的8位同学记为
组,不使用智能手机且成绩优秀的8位同学记为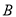 组,计划从
组,计划从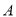 组推选的2人和
组推选的2人和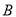 组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自
组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自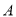 、
、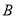 两组的概率.
两组的概率. -
科目: 来源: 题型:
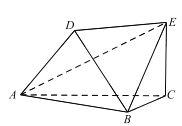
查看答案和解析>>【题目】如图,以
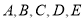 为顶点的六面体中,
为顶点的六面体中, 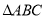 和
和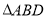 均为等边三角形,且平面
均为等边三角形,且平面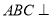 平面
平面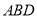 ,
, 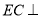 平面
平面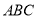 ,
, 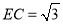 ,
, 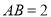 .
.
(1)求证:
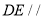 平面
平面 ;
;(2)求此六面体的体积.
相关试题

