【题目】函数![]() 是定义在
是定义在![]() 上的增函数,函数
上的增函数,函数![]() 的图象关于点
的图象关于点![]() 对称.若实数
对称.若实数![]() 满足不等式
满足不等式![]() ,则
,则![]() 的取值范围是_______.
的取值范围是_______.
参考答案:
【答案】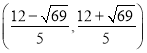
【解析】∵函数y=f(x20)的图象关于点(20,0)对称,
∴函数y=f(x)的图象关于点(0,0)对称,
即函数y=f(x)为奇函数,
则f(x)=f(x),
则不等式f(x26x)+f(y28y+24)<0可化为:
f(x26x)<f(y28y+24)=f(y2+8y24),
又由函数y=f(x)是定义在R上的增函数,
∴x26x<y2+8y24,
即x26x+y28y+24<0,
即(x3)2+(y4)2<1,
则(x,y)点在以(3,4)为圆心,以1为半径的圆内,
目标函数![]() 表示坐标原点与圆上的点连线的斜率,
表示坐标原点与圆上的点连线的斜率,
据此可得:则![]() 的取值范围是
的取值范围是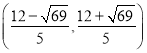 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
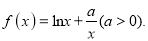
(1)若函数
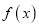 有零点,求实数
有零点,求实数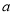 的取值范围;
的取值范围;(2)证明:当
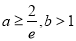 时,
时, 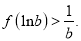
-
科目: 来源: 题型:
查看答案和解析>>【题目】某渔场有一边长为20m的正三角形湖面ABC(如图所示),计划筑一条笔直的堤坝DE将水面分成面积相等的两部分,以便进行两类水产品养殖试验(D在AB上,E在AC上).

(1)为了节约开支,堤坝应尽可能短,请问该如何设计?堤坝最短为多少?
(2)将DE设计为景观路线,堤坝应尽可能长,请问又该如何设计?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,在直角梯形
,在直角梯形 中,
中, 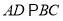 ,
,  ,
,  ,点
,点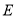 是
是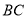 边的中点,将
边的中点,将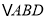 沿
沿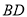 折起,使平面
折起,使平面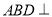 平面
平面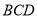 ,连接
,连接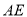 ,
, 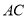 ,
,  ,得到如图
,得到如图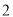 所示的几何体.
所示的几何体.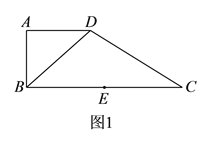
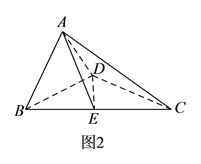
(Ⅰ)求证:
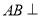 平面
平面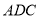 .
.(Ⅱ)若
 ,
, 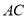 与其在平面
与其在平面 内的正投影所成角的正切值为
内的正投影所成角的正切值为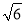 ,求点
,求点 到平面
到平面 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
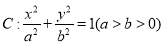 的离心率为
的离心率为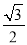 ,且过点
,且过点 .
.(Ⅰ)求椭圆
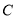 的方程.
的方程.(Ⅱ)若
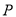 ,
, 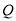 是椭圆
是椭圆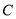 上两个不同的动点,且使
上两个不同的动点,且使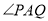 的角平分线垂直于
的角平分线垂直于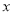 轴,试判断直线
轴,试判断直线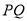 的斜率是否为定值?若是,求出该值;若不是,说明理由.
的斜率是否为定值?若是,求出该值;若不是,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若定义在R上的函数
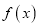 满足
满足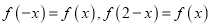 ,且当
,且当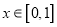 时,
时, 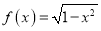 ,则函数
,则函数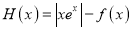 在区间[-7,1]上的零点个数为( )
在区间[-7,1]上的零点个数为( )A. 4 B. 6 C. 8 D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】《中华人民共和国个人所得税》规定,公民月工资、薪金所得不超过3500元的部分不纳税,超过3500元的部分为全月纳税所得额,此项税款按下表分段累计计算:

已知张先生的月工资、薪金所得为10000元,问他当月应缴纳多少个人所得税?
设王先生的月工资、薪金所得为
 元,当月应缴纳个人所得税为
元,当月应缴纳个人所得税为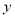 元,写出
元,写出 与
与 的函数关系式;
的函数关系式;(3)已知王先生一月份应缴纳个人所得税为303元,那么他当月的个工资、薪金所得为多少?
相关试题

