【题目】某渔场有一边长为20m的正三角形湖面ABC(如图所示),计划筑一条笔直的堤坝DE将水面分成面积相等的两部分,以便进行两类水产品养殖试验(D在AB上,E在AC上).

(1)为了节约开支,堤坝应尽可能短,请问该如何设计?堤坝最短为多少?
(2)将DE设计为景观路线,堤坝应尽可能长,请问又该如何设计?
参考答案:
【答案】(1)当AD为![]() 时,堤坝最短
时,堤坝最短![]() ;(2)当点D为AB中点或与点B重合时,堤坝最长
;(2)当点D为AB中点或与点B重合时,堤坝最长![]() .
.
【解析】试题分析:
利用题意求得堤坝长的函数解析式结合导函数研究函数的性质可得当AD为![]() 时,堤坝最短
时,堤坝最短![]() ;当点D为AB中点或与点B重合时,堤坝最长
;当点D为AB中点或与点B重合时,堤坝最长![]() .
.
试题解析:
设AD为![]() 米,则
米,则![]() .
.
![]()
![]() ,
,
由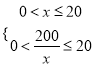 得,
得, ![]() .
.
![]() .
.
令![]() ,
, ![]() ,则
,则![]() ,
,
![]() ,
,
令![]() 得,
得, ![]() ,
, ![]() 得,
得, ![]() ,
,
∴![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
![]() ;
; ![]() ,
,
∴当AD为![]() 时,堤坝最短
时,堤坝最短![]() ;
;
当点D为AB中点或与点B重合时,堤坝最长![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
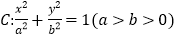 经过点
经过点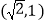 ,且离心率为
,且离心率为 .
.(Ⅰ)求椭圆
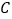 的方程;
的方程;(Ⅱ)设
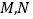 是椭圆上的点,直线
是椭圆上的点,直线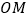 与
与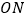 (
(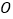 为坐标原点)的斜率之积为
为坐标原点)的斜率之积为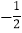 .若动点
.若动点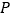 满足
满足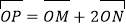 ,试探究是否存在两个定点
,试探究是否存在两个定点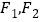 ,使得
,使得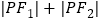 为定值?若存在,求
为定值?若存在,求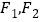 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设A={x|x2-2x=0},B={x|x2-2ax+a2-a=0}.
(1)若A∩B=B,求a的取值范围;
(2)若A∪B=B,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
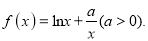
(1)若函数
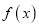 有零点,求实数
有零点,求实数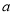 的取值范围;
的取值范围;(2)证明:当
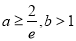 时,
时, 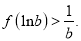
-
科目: 来源: 题型:
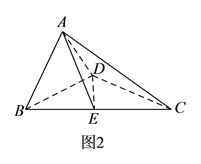
查看答案和解析>>【题目】如图
 ,在直角梯形
,在直角梯形 中,
中, 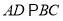 ,
,  ,
,  ,点
,点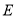 是
是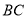 边的中点,将
边的中点,将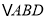 沿
沿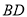 折起,使平面
折起,使平面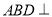 平面
平面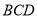 ,连接
,连接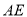 ,
, 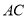 ,
,  ,得到如图
,得到如图 所示的几何体.
所示的几何体.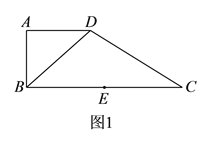
(Ⅰ)求证:
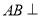 平面
平面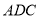 .
.(Ⅱ)若
 ,
, 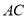 与其在平面
与其在平面 内的正投影所成角的正切值为
内的正投影所成角的正切值为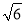 ,求点
,求点 到平面
到平面 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
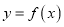 是定义在
是定义在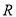 上的增函数,函数
上的增函数,函数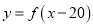 的图象关于点
的图象关于点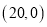 对称.若实数
对称.若实数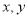 满足不等式
满足不等式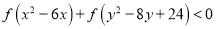 ,则
,则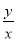 的取值范围是_______.
的取值范围是_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
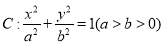 的离心率为
的离心率为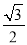 ,且过点
,且过点 .
.(Ⅰ)求椭圆
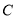 的方程.
的方程.(Ⅱ)若
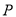 ,
, 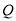 是椭圆
是椭圆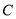 上两个不同的动点,且使
上两个不同的动点,且使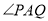 的角平分线垂直于
的角平分线垂直于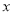 轴,试判断直线
轴,试判断直线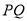 的斜率是否为定值?若是,求出该值;若不是,说明理由.
的斜率是否为定值?若是,求出该值;若不是,说明理由.
相关试题

