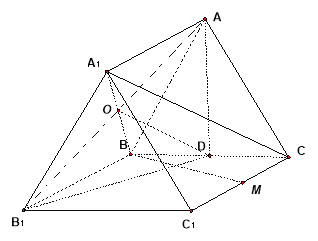
【题目】(本小题满分14分)
在正三棱柱![]() 中,点
中,点![]() 是
是![]() 的中点,
的中点,![]() .
.
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)试在棱![]() 上找一点
上找一点![]() ,使
,使![]() .
.
参考答案:
【答案】(1)详见解析(2)![]() 为
为![]() 的中点.
的中点.
【解析】
试题分析:(1)证明线面平行,一般利用线面平行判定定理进行证明,即先从线线平行出发,这可利用三角形中位线性质进行证明:连接![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,所以
的中点,所以![]() ∥
∥![]() .从而可证
.从而可证![]() ∥平面
∥平面![]() .(2)找一点目的是证线线垂直,故从垂直角度找:利用正方形性质,边的中点与对边顶点连线存在垂直关系,故取
.(2)找一点目的是证线线垂直,故从垂直角度找:利用正方形性质,边的中点与对边顶点连线存在垂直关系,故取![]() 为
为![]() 的中点.再根据线面垂直判定及性质定理进行论证.
的中点.再根据线面垂直判定及性质定理进行论证.
试题解析:(1)证明:连接![]() ,交
,交![]() 于点
于点![]() , 连接
, 连接![]() .
.
∵![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,
∴![]() ∥
∥![]() . 3分
. 3分
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ∥平面
∥平面![]() . 6分
. 6分
(2)![]() 为
为![]() 的中点. 7分
的中点. 7分
证明如下:
∵在正三棱柱![]() 中,
中,![]() ,∴四边形
,∴四边形![]() 是正方形.
是正方形.
∵![]() 为
为![]() 的中点,
的中点,![]() 是
是![]() 的中点,∴
的中点,∴![]() , 9分
, 9分
∴![]() ,
,![]() .
.
又∵![]() ,
,
![]() ,∴
,∴![]() . 11分
. 11分
∵![]() 是正三角形,
是正三角形,![]() 是
是![]() 的中点,
的中点,
∴![]() .
.
∵平面![]() 平面
平面![]() , 平面
, 平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]()
![]() . 13分
. 13分
∵![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() . 14分
. 14分
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分16分)
设函数
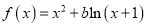 .
.(1)若
 =1时,函数
=1时,函数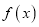 取最小值,求实数
取最小值,求实数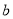 的值;
的值;(2)若函数
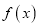 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数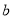 的取值范围;
的取值范围;(3)若
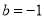 ,证明对任意正整数
,证明对任意正整数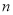 ,不等式
,不等式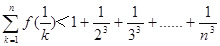 都成立.
都成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
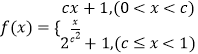 ,且
,且 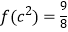 .
.
(1)求实数c的值;
(2)解不等式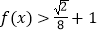 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C的顶点在原点,焦点在x轴上,且抛物线上有一点P(4,m)到焦点的距离为6.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若抛物线C与直线y=kx﹣2相交于不同的两点A、B,且AB中点横坐标为2,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的首项a1=a,Sn是数列{an}的前n项和,且满足:
 =3n2an+
=3n2an+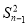 ,an≠0,n≥2,n∈N*.
,an≠0,n≥2,n∈N*.(1)若数列{an}是等差数列,求a的值;
(2)确定a的取值集合M,使a∈M时,数列{an}是递增数列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分14分)
如图,2015年春节,摄影爱好者
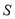 在某公园
在某公园 处,发现正前方
处,发现正前方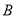 处有一立柱,测得立柱顶端
处有一立柱,测得立柱顶端 的仰角和立柱底部
的仰角和立柱底部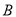 的俯角均为
的俯角均为 ,已知
,已知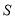 的身高约为
的身高约为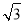 米(将眼睛距地面的距离按
米(将眼睛距地面的距离按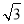 米处理)
米处理)
(1)求摄影者到立柱的水平距离和立柱的高度;
(2)立柱的顶端有一长2米的彩杆
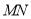 绕中点
绕中点 在
在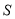 与立柱所在的平面内旋转.摄影者有一视角范围为
与立柱所在的平面内旋转.摄影者有一视角范围为 的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分14分)
设△ABC三个内角A、B、C所对的边分别为a,b,c. 已知C=
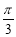 ,acosA=bcosB.
,acosA=bcosB.(1)求角A的大小;
(2)如图,在△ABC的外角∠ACD内取一点P,使得PC=2.过点P分别作直线CA、CD的垂线PM、PN,垂足分别是M、N.设∠PCA=α,求PM+PN的最大值及此时α的取值.


相关试题

