【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点为
,右焦点为![]() 。斜率为1的直线
。斜率为1的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,以
两点,以![]() 为底边作等腰三角形,顶点为
为底边作等腰三角形,顶点为![]() 。
。
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的面积。
的面积。
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)根据椭圆的简单几何性质知![]() ,又
,又![]() ,写出椭圆的方程;(2)先斜截式设出直线
,写出椭圆的方程;(2)先斜截式设出直线![]() ,联立方程组,根据直线与圆锥曲线的位置关系,可得出
,联立方程组,根据直线与圆锥曲线的位置关系,可得出![]() 中点为
中点为![]() 的坐标,再根据△
的坐标,再根据△![]() 为等腰三角形知
为等腰三角形知![]() ,从而得
,从而得![]() 的斜率为
的斜率为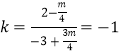 ,求出
,求出![]() ,写出
,写出![]() :
:![]() ,并计算
,并计算![]() ,再根据点到直线距离公式求高,即可计算出面积.
,再根据点到直线距离公式求高,即可计算出面积.
试题解析:(1)由已知得![]() ,
,![]() ,解得
,解得![]() ,又
,又![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,
,
由 得
得![]() ①
①
设![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() (
(![]() ),
),![]() 中点为
中点为![]() ,
,
则![]() ,
,![]() ,
,
因为![]() 是等腰△
是等腰△![]() 的底边,所以
的底边,所以![]() .
.
所以![]() 的斜率为
的斜率为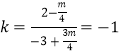 ,解得
,解得![]() ,此时方程①为
,此时方程①为![]() .
.
解得![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,
,
此时,点![]() 到直线
到直线![]() :
:![]() 的距离
的距离![]() ,
,
所以△![]() 的面积
的面积![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 的圆心在
的圆心在 轴上,且经过点
轴上,且经过点 ,
, .
.(Ⅰ)求线段AB的垂直平分线方程;
(Ⅱ)求圆
 的标准方程;
的标准方程;(Ⅲ)过点
 的直线
的直线 与圆
与圆 相交于
相交于 、
、 两点,且
两点,且 ,求直线
,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
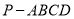 中,PA⊥平面ABCD,CD⊥AD,BC∥AD,
中,PA⊥平面ABCD,CD⊥AD,BC∥AD, .
.
(Ⅰ)求证:CD⊥PD;
(Ⅱ)求证:BD⊥平面PAB;
(Ⅲ)在棱PD上是否存在点M,使CM∥平面PAB,若存在,确定点M的位置,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校高三课外兴趣小组为了解高三同学高考结束后是否打算观看2018年足球世界杯比赛的情况,从全校高三年级1500名男生、1000名女生中按分层抽样的方式抽取125名学生进行问卷调查,情况如下表:
打算观看
不打算观看
女生
20
b
男生
c
25
(1)求出表中数据b,c;
(2)判断是否有99%的把握认为观看2018年足球世界杯比赛与性别有关;
(3)为了计算“从10人中选出9人参加比赛”的情况有多少种,我们可以发现它与“从10人中选出1人不参加比赛”的情况有多少种是一致的.现有问题:在打算观看2018年足球世界杯比赛的同学中有5名男生、2名女生来自高三(5)班,从中推选5人接受校园电视台采访,请根据上述方法,求被推选出的5人中恰有四名男生、一名女生的概率.
P(K2≥k0)
0.10
0.05
0.025
0.01
0.005
K0
2.706
3.841
5.024
6.635
7.879
附:

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
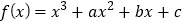 ,那么下列结论中错误的是( )
,那么下列结论中错误的是( )A. 若
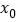 是
是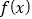 的极小值点,则
的极小值点,则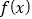 在区间
在区间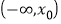 上单调递减
上单调递减B. 函数
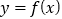 的图像可以是中心对称图形
的图像可以是中心对称图形C.
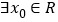 ,使
,使
D. 若
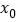 是
是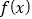 的极值点,则
的极值点,则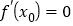
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面几何中,通常将完全覆盖某平面图形且直径最小的圆,称为该平面图形的最小覆盖圆.最小覆盖圆满足以下性质:①线段
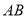 的最小覆盖圆就是以
的最小覆盖圆就是以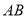 为直径的圆;②锐角
为直径的圆;②锐角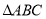 的最小覆盖圆就是其外接圆.已知曲线
的最小覆盖圆就是其外接圆.已知曲线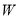 :
: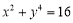 ,
,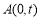 ,
,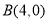 ,
,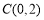 ,
,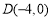 为曲线
为曲线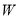 上不同的四点.
上不同的四点.(Ⅰ)求实数
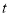 的值及
的值及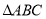 的最小覆盖圆的方程;
的最小覆盖圆的方程;(Ⅱ)求四边形
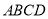 的最小覆盖圆的方程;
的最小覆盖圆的方程;(Ⅲ)求曲线
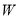 的最小覆盖圆的方程.
的最小覆盖圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班制定了数学学习方案:星期一和星期日分别解决
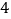 个数学问题,且从星期二开始,每天所解决问题的个数与前一天相比,要么“多一个”要么“持平”要么“少一个”,则在一周中每天所解决问题个数的不同方案共有( )
个数学问题,且从星期二开始,每天所解决问题的个数与前一天相比,要么“多一个”要么“持平”要么“少一个”,则在一周中每天所解决问题个数的不同方案共有( )A.
 种 B.
种 B. 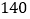 种 C.
种 C. 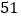 种 D.
种 D. 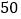 种
种
相关试题

