【题目】已知函数f(x)=3x+λ3﹣x(λ∈R)
(1)当λ=﹣4时,求解方程f(x)=3;
(2)根据λ的不同取值,讨论函数的奇偶性,并说明理由.
参考答案:
【答案】
(1)解:当λ=﹣4时,由f(x)=3,得3x﹣43﹣x=3.
令t=3x>0,则原方程可化为t2﹣3t﹣4=0,解得t=4,或t=﹣1(舍去),
所以,x=log34
(2)解:函数 的定义域为R,当λ=1时,f(x)=3x+3﹣x,f(﹣x)=f(x),
函数为偶函数;
当λ=﹣1时,f(x)=3x﹣3﹣x,f(﹣x)=﹣f(x),函数为奇函数;
当|λ|≠1时, ![]() ,
,
此时f(﹣1)≠﹣f(1)且f(﹣1)≠f(1),所以函数为非奇非偶函数
【解析】(1)当λ=﹣4时,令t=3x>0,则原方程可化为t2﹣3t﹣4=0,求得t的值,可得x的值.(2)函数的定义域为R,分当λ=1、当λ=﹣1、当|λ|≠1三种情况,分别根据奇偶函数的定义进行判断,可得结论.
【考点精析】本题主要考查了函数的奇偶性的相关知识点,需要掌握偶函数的图象关于y轴对称;奇函数的图象关于原点对称才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是定义在
是定义在 上的奇函数,且对任意实数
上的奇函数,且对任意实数 ,恒有
,恒有 ,当
,当 时,
时, 
(1)求证:
 是周期函数;
是周期函数;(2)当
 时,求
时,求 的解析式;
的解析式;(3)计算

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

 在
在 上单调递增,
上单调递增,(1)若函数
 有实数零点,求满足条件的实数
有实数零点,求满足条件的实数 的集合
的集合 ;
;(2)若对于任意的
 时,不等式
时,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
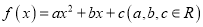 对任意实数
对任意实数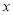 ,都有
,都有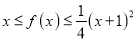 恒成立.
恒成立.(Ⅰ)证明:
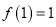 ;
;(Ⅱ)若
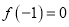 ,求
,求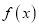 的表达式;
的表达式;(Ⅲ)在题(Ⅱ)的条件下设
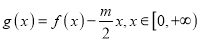 ,若
,若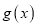 图象上的点都位于直线
图象上的点都位于直线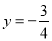 的上方,求实数
的上方,求实数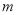 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在公比为正数的等比数列{an}中,
 ,
,  ,数列{bn}(bn>0)的前n项和为Sn满足
,数列{bn}(bn>0)的前n项和为Sn满足  (n≥2),且S10=100.
(n≥2),且S10=100.
( I)求数列{an}和数列{bn}的通项公式;
( II)求数列{anbn}的前n项和为Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,AB=
 ,BC=1,P为△ABC内一点,∠BPC=90°.
,BC=1,P为△ABC内一点,∠BPC=90°. 
(1)若PB= ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA. -
科目: 来源: 题型:
查看答案和解析>>【题目】设S表示所有大于﹣1的实数构成的集合,确定所有的函数:S→S,满足以下两个条件:
对于S内的所有x和y,f(x+f(y)+xf(y))=y+f(x)+yf(x);在区间﹣1<x<0与x>0的每一个内, 是严格递增的.求满足上述条件的函数的方程.
是严格递增的.求满足上述条件的函数的方程.
相关试题

