【题目】设![]() 是定义在
是定义在![]() 上的奇函数,且对任意实数
上的奇函数,且对任意实数![]() ,恒有
,恒有![]() ,当
,当![]() 时,
时, ![]()
(1)求证: ![]() 是周期函数;
是周期函数;
(2)当![]() 时,求
时,求![]() 的解析式;
的解析式;
(3)计算![]()
参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)根据条件利用![]() 是定义在
是定义在![]() 上的奇函数,
上的奇函数, ![]() ,可得
,可得![]() ,从而证得结论;(2)利用函数的奇偶性和周期性,求得当
,从而证得结论;(2)利用函数的奇偶性和周期性,求得当![]() 时,函数
时,函数![]() 的解析式;(3)利用周期为
的解析式;(3)利用周期为![]() 以及
以及![]() 的值,可得
的值,可得![]() 的值.
的值.
试题解析:(1)证明:∵![]() ,∴
,∴![]() .∴
.∴![]() 是周期为4的周期函数.
是周期为4的周期函数.
(2)∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,即
,即![]()
(3)∵![]()
又![]() 是周期为4的周期函数,
是周期为4的周期函数,
![]()
![]()
【方法点晴】本题主要考查函数的解析式及函数的周期性,属于难题.对函数周期性的考查主要命题方向由两个,一是三角函数,可以用公式求出周期;二是抽象函数,往往需要根据条件判断出周期,抽象函数给出条件判断周期的常见形式为:
(1) ![]() ;(2)
;(2)![]() ;
;
(3) ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】长春市的“名师云课”活动自开展以来获得广大家长和学生的高度赞誉,在我市推出的第二季名师云课中,数学学科共计推出36节云课,为了更好地将课程内容呈现给学生,现对某一时段云课的点击量进行统计:
点击量



节数
6
18
12
(Ⅰ)现从36节云课中采用分层抽样的方式选出6节,求选出的点击量超过3000的节数.
(Ⅱ)为了更好地搭建云课平台,现将云课进行剪辑,若点击量在区间
 内,则需要花费40分钟进行剪辑,若点击量在区间
内,则需要花费40分钟进行剪辑,若点击量在区间 内,则需要花费20分钟进行剪辑,点击量超过3000,则不需要剪辑,现从(Ⅰ)中选出的6节课中随机取出2节课进行剪辑,求剪辑时间
内,则需要花费20分钟进行剪辑,点击量超过3000,则不需要剪辑,现从(Ⅰ)中选出的6节课中随机取出2节课进行剪辑,求剪辑时间 的分布列与数学期望.
的分布列与数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn满足Sn=
 n2+
n2+  n(n∈N*),数列{bn}是首项为4的正项等比数列,且2b2 , b3﹣3,b2+2成等差数列. (Ⅰ)求数列{an},{bn}的通项公式;
n(n∈N*),数列{bn}是首项为4的正项等比数列,且2b2 , b3﹣3,b2+2成等差数列. (Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)令cn=anbn(n∈N*),求数列{cn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
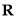 上的函数
上的函数 满足:函数
满足:函数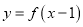 的图象关于直线
的图象关于直线 对称,且当
对称,且当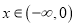 时
时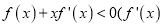 是函数
是函数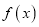 的导函数)成立.若
的导函数)成立.若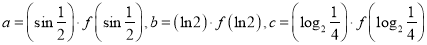 ,则
,则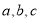 的大小关系是
的大小关系是A.
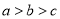 B.
B. 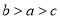 C.
C. 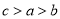 D.
D. 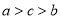
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

 在
在 上单调递增,
上单调递增,(1)若函数
 有实数零点,求满足条件的实数
有实数零点,求满足条件的实数 的集合
的集合 ;
;(2)若对于任意的
 时,不等式
时,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
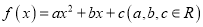 对任意实数
对任意实数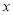 ,都有
,都有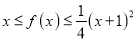 恒成立.
恒成立.(Ⅰ)证明:
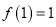 ;
;(Ⅱ)若
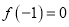 ,求
,求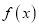 的表达式;
的表达式;(Ⅲ)在题(Ⅱ)的条件下设
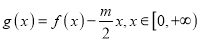 ,若
,若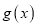 图象上的点都位于直线
图象上的点都位于直线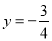 的上方,求实数
的上方,求实数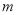 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=3x+λ3﹣x(λ∈R)
(1)当λ=﹣4时,求解方程f(x)=3;
(2)根据λ的不同取值,讨论函数的奇偶性,并说明理由.
相关试题

