【题目】已知关于x的方程x2-2mx+4m2-6=0的两不等根为α,β,试求(α-1)2+(β-1)2的最值.
参考答案:
【答案】最大值为15,无最小值.
【解析】试题分析:根据一元二次方程写出韦达定理,将原式化简为两根和与乘积的形式代入,化简为关于m的二次函数,由Δ>0求出m的取值范围,即函数的定义域,根据二次函数的图象和性质求出最值.
试题解析:
由题可知α+β=2m,αβ=4m2-6,
∴(α-1)2+(β-1)2=α2+β2-2(α+β)+2=(α+β)2-2αβ-2(α+β)+2
=4m2-2(4m2-6)-2·2m+2=-4m2-4m+14=-4(m+![]() )2+15.
)2+15.
∵Δ=(-2m)2-4(4m2-6)=-12m2+24>0,∴当m=-![]() 时满足Δ>0.∴原式的最大值为15,无最小值.
时满足Δ>0.∴原式的最大值为15,无最小值.
点睛:本题考查一元二次方程根与系数的关系.设一元二次方程![]() 的两根为
的两根为![]() ,
, ![]() ,当
,当![]() 时,方程有两个等根,当
时,方程有两个等根,当![]() 时,方程无根, 当
时,方程无根, 当![]() 时,方程有两个不相等的实数根,且根据韦达定理有
时,方程有两个不相等的实数根,且根据韦达定理有![]() ,或者根据求根公式可得
,或者根据求根公式可得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】心理学家分析发现“喜欢空间想象”与“性别”有关,某数学兴趣小组为了验证此结论,从全体组员中按分层抽样的方法抽取50名同学(男生30人、女生20人),给每位同学立体几何题、代数题各一道,让各位同学自由选择一道题进行解答,选题情况统计如下表:(单位:人)
立体几何题
代数题
总计
男同学
22
8
30
女同学
8
12
20
总计
30
20
50
(1)能否有97.5%以上的把握认为“喜欢空间想象”与“性别”有关?
(2)经统计得,选择做立体几何题的学生正答率为
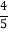 ,且答对的学生中男生人数是女生人数的5倍,现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究,求恰好抽到男女生各一人的概率.
,且答对的学生中男生人数是女生人数的5倍,现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究,求恰好抽到男女生各一人的概率.附表及公式:
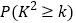
0.15
0.10
0.05
0.025
0.010
0.005
0.001
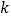
2.072
2.706
3.841
5.024
6.635
7.879
10.828
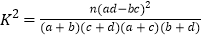
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
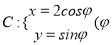 为参数),
为参数), 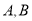 是
是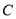 上的动点,且满足
上的动点,且满足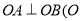 为坐标原点),以原点
为坐标原点),以原点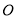 为极点,
为极点, 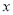 轴的正半轴为极轴建立坐标系,点
轴的正半轴为极轴建立坐标系,点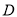 的极坐标为
的极坐标为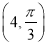 .
.(1)求线段
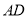 的中点
的中点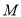 的轨迹
的轨迹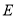 的普通方程;
的普通方程;(2)利用椭圆
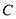 的极坐标方程证明
的极坐标方程证明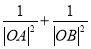 为定值,并求面积的最大值.
为定值,并求面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】现在颈椎病患者越来越多,甚至大学生也出现了颈椎病,年轻人患颈椎病多与工作、生活方式有关,某调查机构为了了解大学生患有颈椎病是否与长期过度使用电子产品有关,在遂宁市中心医院随机的对入院的50名大学生进行了问卷调查,得到了如下的4×4列联表:
未过度使用
过度使用
合计
未患颈椎病
15
5
20
患颈椎病
10
20
30
合计
25
25
50
(1)是否有99.5%的把握认为大学生患颈锥病与长期过度使用电子产品有关?
(2)已知在患有颈锥病的10名未过度使用电子产品的大学生中,有3名大学生又患有肠胃炎,现在从上述的10名大学生中,抽取3名大学生进行其他方面的排查,记选出患肠胃炎的学生人数为
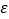 ,求
,求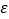 的分布列及数学期望.
的分布列及数学期望.参考数据与公式:
P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
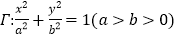 的右焦点与短轴两端点构成一个面积为2的等腰直角三角形,
的右焦点与短轴两端点构成一个面积为2的等腰直角三角形, 为坐标原点.
为坐标原点.(1)求椭圆
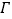 的方程;
的方程;(2)设点
 在椭圆
在椭圆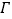 上,点
上,点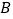 在直线
在直线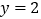 上,且
上,且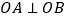 ,求证:
,求证: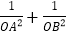 为定值;
为定值;(3)设点
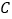 在椭圆
在椭圆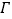 上运动,
上运动,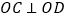 ,且点
,且点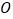 到直线
到直线 的距离为常数
的距离为常数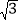 ,求动点
,求动点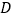 的轨迹方程.
的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x),当x,y∈R时,恒有f(x+y)=f(x)+f(y).当x>0时,f(x)>0.
(1)求证:f(x)是奇函数;
(2)若f(1)=
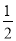 ,试求f(x)在区间[-2,6]上的最值.
,试求f(x)在区间[-2,6]上的最值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了让贫困地区的孩子们过一个温暖的冬天,某校阳光志愿者社团组织“这个冬天不再冷”冬衣募捐活动,共有50名志愿者参与.志愿者的工作内容有两项:①到各班做宣传,倡议同学们积极捐献冬衣;②整理、打包募捐上来的衣物.每位志愿者根据自身实际情况,只参与其中的某一项工作.相关统计数据如下表所示:

(1)如果用分层抽样的方法从参与两项工作的志愿者中抽取5人,再从这5人中选2人,那么“至少有1人是参与班级宣传的志愿者”的概率是多少?
(2)若参与班级宣传的志愿者中有12名男生,8名女生,从中选出2名志愿者,用
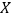 表示所选志愿者中的女生人数,写出随机变量
表示所选志愿者中的女生人数,写出随机变量 的分布列及数学期望.
的分布列及数学期望.
相关试题

