【题目】已知椭圆![]() 的右焦点与短轴两端点构成一个面积为2的等腰直角三角形,
的右焦点与短轴两端点构成一个面积为2的等腰直角三角形,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() ,求证:
,求证:![]() 为定值;
为定值;
(3)设点![]() 在椭圆
在椭圆![]() 上运动,
上运动,![]() ,且点
,且点![]() 到直线
到直线![]() 的距离为常数
的距离为常数![]() ,求动点
,求动点![]() 的轨迹方程.
的轨迹方程.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)由椭圆的右焦点与短轴两端点构成一个面积为![]() 的等腰直角三角形,求出
的等腰直角三角形,求出![]() ,可得椭圆方程;(2)设
,可得椭圆方程;(2)设![]() ,则
,则![]() 的方程为:
的方程为:![]() ,由
,由![]() 得
得![]() 点坐标,可证明
点坐标,可证明![]() .(3) 设
.(3) 设![]() ,由
,由![]() 得
得![]() ,又
,又![]() 点在椭圆上得:
点在椭圆上得:![]() ,从而
,从而![]()
![]() 化简可得
化简可得![]() 的轨迹方程.
的轨迹方程.
试题解析:
解:(1)由条件可得![]() ,
,![]()
椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,则
,则![]() 的方程为:
的方程为:![]() ,
,
由![]() 得:
得:![]()
所以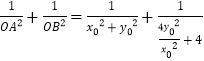
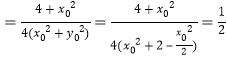 .
.
(3)设![]() ,由
,由![]() 得
得![]() ①
①
又![]() 点在椭圆上得:
点在椭圆上得:![]() ②
②
联立①②可得![]() ,
,![]() ③
③
由![]() 得
得![]() ,
,
即![]()
可得![]() ,
,
将③代入得:
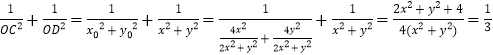
化简得![]() 点轨迹方程为:
点轨迹方程为:![]() .
.
点睛:本题考查圆锥曲线的标准方程,曲线与方程,直线与椭圆的位置关系以及定值问题,属于中档题目.证明定值问题,先设出![]() 点坐标,根据
点坐标,根据![]() 求出直线
求出直线![]() 的方程,再根据
的方程,再根据![]() 点在
点在![]() 上求出坐标, 证明
上求出坐标, 证明![]() 为定值,利用两点间距离公式代入坐标,根据点在曲线上两元换一元,分子分母成倍数关系,即为定值.
为定值,利用两点间距离公式代入坐标,根据点在曲线上两元换一元,分子分母成倍数关系,即为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
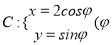 为参数),
为参数), 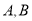 是
是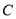 上的动点,且满足
上的动点,且满足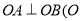 为坐标原点),以原点
为坐标原点),以原点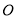 为极点,
为极点, 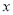 轴的正半轴为极轴建立坐标系,点
轴的正半轴为极轴建立坐标系,点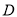 的极坐标为
的极坐标为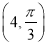 .
.(1)求线段
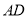 的中点
的中点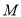 的轨迹
的轨迹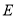 的普通方程;
的普通方程;(2)利用椭圆
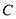 的极坐标方程证明
的极坐标方程证明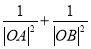 为定值,并求面积的最大值.
为定值,并求面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】现在颈椎病患者越来越多,甚至大学生也出现了颈椎病,年轻人患颈椎病多与工作、生活方式有关,某调查机构为了了解大学生患有颈椎病是否与长期过度使用电子产品有关,在遂宁市中心医院随机的对入院的50名大学生进行了问卷调查,得到了如下的4×4列联表:
未过度使用
过度使用
合计
未患颈椎病
15
5
20
患颈椎病
10
20
30
合计
25
25
50
(1)是否有99.5%的把握认为大学生患颈锥病与长期过度使用电子产品有关?
(2)已知在患有颈锥病的10名未过度使用电子产品的大学生中,有3名大学生又患有肠胃炎,现在从上述的10名大学生中,抽取3名大学生进行其他方面的排查,记选出患肠胃炎的学生人数为
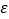 ,求
,求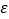 的分布列及数学期望.
的分布列及数学期望.参考数据与公式:
P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2-2mx+4m2-6=0的两不等根为α,β,试求(α-1)2+(β-1)2的最值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x),当x,y∈R时,恒有f(x+y)=f(x)+f(y).当x>0时,f(x)>0.
(1)求证:f(x)是奇函数;
(2)若f(1)=
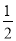 ,试求f(x)在区间[-2,6]上的最值.
,试求f(x)在区间[-2,6]上的最值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了让贫困地区的孩子们过一个温暖的冬天,某校阳光志愿者社团组织“这个冬天不再冷”冬衣募捐活动,共有50名志愿者参与.志愿者的工作内容有两项:①到各班做宣传,倡议同学们积极捐献冬衣;②整理、打包募捐上来的衣物.每位志愿者根据自身实际情况,只参与其中的某一项工作.相关统计数据如下表所示:

(1)如果用分层抽样的方法从参与两项工作的志愿者中抽取5人,再从这5人中选2人,那么“至少有1人是参与班级宣传的志愿者”的概率是多少?
(2)若参与班级宣传的志愿者中有12名男生,8名女生,从中选出2名志愿者,用
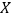 表示所选志愿者中的女生人数,写出随机变量
表示所选志愿者中的女生人数,写出随机变量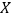 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地政府决定建造一批保障房供给社会,缓解贫困人口的住房问题,计划用1 600万元购得一块土地,在该土地上建造10幢楼房的住宅小区,每幢楼的楼层数相同,且每层建筑面积均为1 000平方米,每平方米的建筑费用与楼层有关,第x层楼房每平方米的建筑费用为(kx+800)元(其中k为常数).经测算,若每幢楼为5层,则该小区每平方米的平均综合费用为1 270元.
注:每平方米平均综合费用=
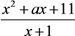 .
.(1) 求k的值;
(2) 问要使该小区楼房每平方米的平均综合费用最低,应将这10幢楼房建成多少层?此时每平方米的平均综合费用为多少元?
相关试题

