【题目】设f(x)=![]() (m>0,n>0).
(m>0,n>0).
(1) 当m=n=1时,求证:f(x)不是奇函数;
(2) 设f(x)是奇函数,求m与n的值;
(3) 在(2)的条件下,求不等式f(f(x))+f![]() <0的解集.
<0的解集.
参考答案:
【答案】(1)见解析(2)![]() (3)(-∞,log23).
(3)(-∞,log23).
【解析】试题分析:(1)只要举一个反例说明f(x)不是奇函数即可(2)由奇函数性质得恒等式,再根据恒等式定理得对应项系数为零,解方程组可得m与n的值;注意验证函数定义域关于零点对称(3)先分离函数,判定函数单调性,再利用奇偶性以及单调性化简不等式f(f(x))+f![]() <0为f(x)>-
<0为f(x)>-![]() ,最后最后为指数函数不等式: 2x<3,解得x<log23即为所求
,最后最后为指数函数不等式: 2x<3,解得x<log23即为所求
试题解析:(1) 证明:因为当m=n=1时,f(x)=![]() ,f(1)=-
,f(1)=-![]() ,f(-1)=
,f(-1)=![]() , f(-1)≠-f(1),所以f(x)不是奇函数.
, f(-1)≠-f(1),所以f(x)不是奇函数.
(2) 解:当f(x)是奇函数时,f(-x)=-f(x),即![]() =-
=-![]() 对定义域内任意实数x成立.
对定义域内任意实数x成立.
化简整理得(2m-n)·22x+(2mn-4)·2x+(2m-n)=0,这是关于x的恒等式,
所以![]()
所以![]() (不符,舍去)或
(不符,舍去)或![]()
经检验![]() 符合题意,所以
符合题意,所以![]()
(3) 解:由(2)可知f(x)=![]() =
=![]() (-1+
(-1+![]() ),易判断f(x)是R上单调减函数;
),易判断f(x)是R上单调减函数;
由f(f(x))+f(![]() )<0,得f(f(x))<f
)<0,得f(f(x))<f![]() f(x)>-
f(x)>-![]() 2x<3 x<log23,
2x<3 x<log23,
所以f(x)>0的解集为(-∞,log23).
-
科目: 来源: 题型:
查看答案和解析>>【题目】条件
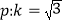 ;条件
;条件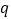 :直线
:直线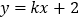 与圆
与圆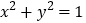 相切,则
相切,则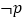 是
是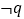 的( )
的( )A. 充分必要条件 B. 必要不充分条件
C. 充分不必要条件 D. 既不充分也不必要条件
-
科目: 来源: 题型:
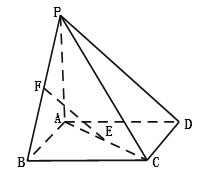
查看答案和解析>>【题目】如图,四棱锥
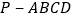 的底面
的底面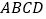 为正方形,
为正方形,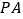 ⊥底面
⊥底面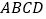 ,
,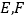 分别是
分别是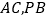 的中点,
的中点,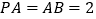 .
.
(Ⅰ)求证
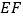 ∥平面
∥平面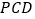 ;
;(Ⅱ)求直线
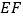 与平面
与平面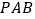 所成的角;
所成的角;(Ⅲ)求四棱锥
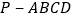 的外接球的体积.
的外接球的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
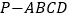 中,底面
中,底面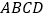 为平行四边形,
为平行四边形, 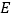 为侧棱
为侧棱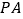 的中点.
的中点.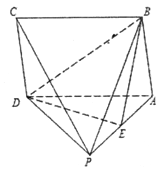
(Ⅰ)求证:
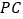 ∥平面
∥平面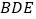
(Ⅱ)若
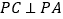 ,
,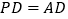 ,
,求证:平面
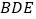
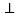 平面
平面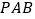
-
科目: 来源: 题型:
查看答案和解析>>【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
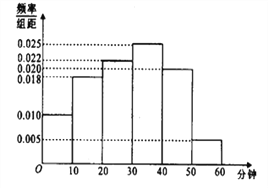
(Ⅰ)根据已知条件完成下面的
 列联表,并据此资料判断你是否有95%以上的把握认为“体育迷”与性别有关?
列联表,并据此资料判断你是否有95%以上的把握认为“体育迷”与性别有关?非体育迷
体育迷
合计
男
女
合计
(参考公式
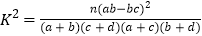 ,其中
,其中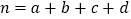 .)
.)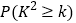
0.050
0.010
0.001
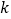
3.841
6.635
10.828
(Ⅱ)将日均收看该体育项目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某初级中学有三个年级,各年级男、女人数如下表:
初一年级
初二年级
初三年级
女生
370
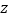
200
男生
380
370
300
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求
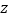 的值;
的值;(2)用分层抽样的方法在初三年级中抽取一个容量为5的样本,求该样本中女生的人数;
(3)用随机抽样的方法从初二年级女生中选出8人,测量它们的左眼视力,结果如下:1.2,1.5,1.2,1.5,1.5,1.3,1.0,1.2.把这8人的左眼视力看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.1的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x0,x0+
 是函数f(x)=cos2(wx﹣
是函数f(x)=cos2(wx﹣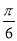 )﹣sin2wx(ω>0)的两个相邻的零点
)﹣sin2wx(ω>0)的两个相邻的零点(1)求
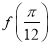 的值;
的值;(2)若对任意
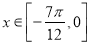 ,都有f(x)﹣m≤0,求实数m的取值范围.
,都有f(x)﹣m≤0,求实数m的取值范围.(3)若关于
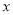 的方程
的方程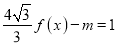 在
在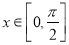 上有两个不同的解,求实数
上有两个不同的解,求实数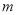 的取值范围.
的取值范围.
相关试题

