【题目】在钝角△ABC中,角A,B,C所对的边分别为a,b,c且b=atanB. (Ⅰ)求A﹣B的值;
(Ⅱ)求cos2B﹣sinA的取值范围.
参考答案:
【答案】解:(Ⅰ)由b=atanB得:bcosB=asinB 又由正弦定理得,sinBcosB=sinAsinB,
所以cosB=sinA
又△ABC是钝角三角形,所以 ![]() .
.
(Ⅱ)由(Ⅰ)知 ![]()
又由 ![]() ,所以
,所以 ![]() ,
,
所以 ![]() ,
, ![]()
又由于函数 ![]() 在
在 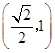 上单调递增,
上单调递增,
所以cos2B﹣sinA的取值范围为 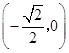 .
.
【解析】(Ⅰ)由b=atanB得:bcosB=asinB,再利用正弦定理即可得出.(Ⅱ)由(Ⅰ)知 ![]() ,利用二次函数的单调性、三角函数的单调性与值域即可得出.
,利用二次函数的单调性、三角函数的单调性与值域即可得出.
【考点精析】掌握正弦定理的定义是解答本题的根本,需要知道正弦定理:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解学生对数学学案质量的满意度,从高一、高二两个年级分别随机调查了20个学生,得到对学案满意度评分(满分100分)的茎叶图如图:则下列说法错误的是( )

A.高一学生满意度评分的平均值比高二学生满意度评分的平均值高
B.高一学生满意度评分比较集中,高二学生满意度评分比较分散
C.高一学生满意度评分的中位数为80
D.高二学生满意度评分的中位数为74 -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=sin(ωx+φ)+
 的图象过(1,2),若f(x)相邻的零点为x1 , x2且满足|x1﹣x2|=6,则f(x)的单调增区间为( )
的图象过(1,2),若f(x)相邻的零点为x1 , x2且满足|x1﹣x2|=6,则f(x)的单调增区间为( )
A.[﹣2+12k,4+12k](k∈Z)
B.[﹣5+12k,1+12k](k∈Z)
C.[1+12k,7+12k](k∈Z)
D.[﹣2+6k,1+6k](k∈Z) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)对任意的x∈R,都有f(﹣x)+f(x)=﹣6,且当x≥0时,f(x)=2x﹣4,定义在R上的函数g(x)=a(x﹣a)(x+a+1),两函数同时满足:x∈R,都有f(x)<0或g(x)<0;x∈(﹣∞,﹣1),f(x)g(x)<0,则实数a的取值范围为( )
A.(﹣3,0)
B.
C.(﹣3,﹣1)
D.(﹣3,﹣1] -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在道路边安装路灯,路面
 宽
宽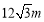 ,灯柱
,灯柱 高14
高14 ,灯杆
,灯杆 与地面所成角为30°.路灯采用锥形灯罩,灯罩轴线
与地面所成角为30°.路灯采用锥形灯罩,灯罩轴线 与灯杆
与灯杆 垂直,轴线
垂直,轴线 ,灯杆
,灯杆 都在灯柱
都在灯柱 和路面宽线
和路面宽线 确定的平面内.
确定的平面内.
(1)当灯杆
 长度为多少时,灯罩轴线
长度为多少时,灯罩轴线 正好通过路面
正好通过路面 的中线?
的中线?(2)如果灯罩轴线AC正好通过路面
 的中线,此时有一高2.5
的中线,此时有一高2.5  的警示牌直立在
的警示牌直立在 处,求警示牌在该路灯灯光下的影子长度.
处,求警示牌在该路灯灯光下的影子长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰梯形ABCD中,AD∥BC,BC=2AD=2AB=4,将△ABD沿BD折到△A′BD的位置,使平面A′BD⊥平面CBD.

(Ⅰ)求证:CD⊥A′B;
(Ⅱ)试在线段A′C上确定一点P,使得二面角P﹣BD﹣C的大小为45°. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校举办“中国诗词大赛”活动,某班派出甲乙两名选手同时参加比赛.大赛设有15个诗词填空题,其中“唐诗”、“宋词”和“毛泽东诗词”各5个.每位选手从三类诗词中各任选1个进行作答,3个全答对选手得3分,答对2个选手得2分,答对1个选手得1分,一个都没答对选手得0分.已知“唐诗”、“宋词”和“毛泽东诗词”中甲能答对的题目个数依次为5,4,3,乙能答对的题目个数依此为4,5,4,假设每人各题答对与否互不影响,甲乙两人答对与否也互不影响. 求:
(Ⅰ)甲乙两人同时得到3分的概率;
(Ⅱ)甲乙两人得分之和ξ的分布列和数学期望.
相关试题

