【题目】已知函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)记![]() 的最大值为
的最大值为![]() ,若
,若![]() 且
且![]() ,求证:
,求证:![]() ;
;
(3)若![]() ,记集合
,记集合![]() 中的最小元素为
中的最小元素为![]() ,设函数
,设函数![]() ,求证:
,求证:![]() 是
是![]() 的极小值点.
的极小值点.
参考答案:
【答案】(1)增区间为![]() ,减区间为
,减区间为![]() ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
【解析】分析:(1)分别解不等式![]() 和
和![]() 可得
可得![]() 的增区间和减区间.
的增区间和减区间.
(2)![]() ,根据
,根据![]() 得到
得到![]() ,把该式变形为
,把该式变形为 ,证明函数不等式
,证明函数不等式![]() 在
在![]() 恒成立即可.
恒成立即可.
(3)根据(1)中函数的单调性及![]() 可得
可得![]() ,因此
,因此 ,分别讨论函数在
,分别讨论函数在![]() 的单调性可判断
的单调性可判断![]() 是
是![]() 的极小值点.
的极小值点.
详解:(1)![]() ,
,
因为![]() 由
由![]() ,得
,得![]() ;
;
由![]() ,得
,得![]() ;
;
所以,![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() .
.
(2)由(1)知,![]() .
.
∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴ ![]() ,∴
,∴ ,
,
设![]() ,则
,则![]() ,
,
所以,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,则
,则![]() ,因
,因![]() ,
,
故![]() ,
, ,所以
,所以![]() .
.
(3)由(1)可知,![]() 在区间
在区间![]() 单调递增,又
单调递增,又![]() 时,
时,![]() ,
,
易知,![]() 在
在![]() 递增,
递增,![]() ,
,
∴![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
当![]() 时,
时,
于是![]() 时,
时,![]() , (所以,若证明
, (所以,若证明![]() ,便能证明
,便能证明![]() ),
),
记![]() ,
,
则![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 内单调递增,∴
内单调递增,∴![]() ,
,
∵![]() ,
,
∴![]() 在
在![]() 内单调递增.
内单调递增.
∴![]() ,于是
,于是![]() 时,
时,
![]() ,
,
∴![]() 在
在![]() 递减.
递减.
当![]() 时,相应的
时,相应的![]() ,
,
∴![]() 在
在![]() 递增.故
递增.故![]() 是
是![]() 的极小值点.
的极小值点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是正四面体的平面展开图,
 分别是
分别是 的中点,在这个正四面体中:①
的中点,在这个正四面体中:① 与
与 平行;②
平行;② 与
与 为异面直线;③
为异面直线;③ 与
与 成60°角;④
成60°角;④ 与
与 垂直.以上四个命题中,正确命题的个数是( )
垂直.以上四个命题中,正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为 ,点
,点 为椭圆上一点.
为椭圆上一点. (1)求椭圆C的方程;
(2)已知两条互相垂直的直线
 ,
, 经过椭圆
经过椭圆 的右焦点
的右焦点 ,与椭圆
,与椭圆 交于
交于 四点,求四边形
四点,求四边形 面积的的取值范围.
面积的的取值范围. -
科目: 来源: 题型:
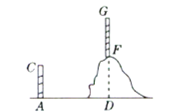
查看答案和解析>>【题目】如图,要测量山顶上的电视塔FG的高度,已知山的西面有一栋楼AC(该楼的高度低于山的高度).试设计在楼AC上测山顶电视塔高度的测量、计算方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在某海滨城市A附近的海面出现台风活动.据监测,目前台风中心位于城市A的东偏南60°方向、距城市A300km的海面点P处,并以20km/h的速度向西偏北30°方向移动.如果台风影响的范围是以台风中心为圆心的圆形区域,半径为
 km,将问题涉及范围内的地球表面看成平面,判断城市A是否会受到上述台风的影响.如果会,求出受影响的时间;如果不会,说明理由.
km,将问题涉及范围内的地球表面看成平面,判断城市A是否会受到上述台风的影响.如果会,求出受影响的时间;如果不会,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设三个数
 成等差数列,记
成等差数列,记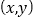 对应点的曲线是
对应点的曲线是 .
.(1)求曲线
 的方程;
的方程;(2)已知点
 ,点
,点 ,点
,点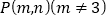 ,过点
,过点 任作直线
任作直线 与曲线
与曲线 相交于
相交于 两点,设直线
两点,设直线 的斜率分别为
的斜率分别为 ,若
,若 ,求
,求 满足的关系式.
满足的关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】某渔船在航行中不幸遇险,发出呼叫信号,我海军舰艇在
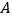 处获悉后,立即测出该渔船在方位角(从指北方向顺时针转到目标方向线的水平角)为
处获悉后,立即测出该渔船在方位角(从指北方向顺时针转到目标方向线的水平角)为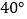 ,距离为15海里的
,距离为15海里的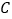 处,并测得渔船正沿方位角为
处,并测得渔船正沿方位角为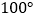 的方向,以15海里/小时的速度向小岛
的方向,以15海里/小时的速度向小岛 靠拢,我海军舰艇立即以
靠拢,我海军舰艇立即以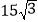 海里/小时的速度前去营救,求舰艇靠近渔船所需的最少时间和舰艇的航向.
海里/小时的速度前去营救,求舰艇靠近渔船所需的最少时间和舰艇的航向.
相关试题

