【题目】在直角坐标系xOy中,曲线C1: ![]() (t为参数,t≠0),其中0≤α<π.在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sin θ,C3:ρ=2
(t为参数,t≠0),其中0≤α<π.在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sin θ,C3:ρ=2![]() cos θ.
cos θ.
(1)求C2与C3交点的直角坐标;
(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|的最大值.
参考答案:
【答案】(1)(0,0)和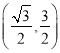 .(2)4.
.(2)4.
【解析】试题分析:(1)将![]() 与
与![]() 转化为直角坐标方程,解方程组即可求出交点坐标;(2)求出
转化为直角坐标方程,解方程组即可求出交点坐标;(2)求出![]() ,
, ![]() 的极坐标,利用距离公式进行求解.
的极坐标,利用距离公式进行求解.
试题解析:(1)曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
联立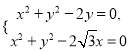 解得
解得![]() 或
或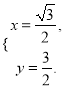
所以![]() 与
与![]() 交点的直角坐标为
交点的直角坐标为![]() 和
和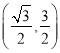
(2)曲线![]() 的极坐标方程为
的极坐标方程为![]() ,其中
,其中![]()
因此![]() 的极坐标为
的极坐标为![]() ,
, ![]() 的极坐标为[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2016/6/1/1572680658870272/1572680665268224/EXPLANATION/e9b48f59939d4f508c427ac0fd6678ec.png]
的极坐标为[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2016/6/1/1572680658870272/1572680665268224/EXPLANATION/e9b48f59939d4f508c427ac0fd6678ec.png]
所以![]()
当![]() 时,
时, ![]() 取得最大值,最大值为4
取得最大值,最大值为4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)的导函数f′(x),且对任意x>0,都有f′(x)>
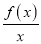 .
.(1)判断函数F(x)=
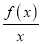 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;(2)设x1,x2∈(0,+∞),证明:f(x1)+f(x2)<f(x1+x2);
(3)请将(2)中结论推广到一般形式,并证明你所推广的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y=
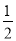 x上时,求直线AB的方程.
x上时,求直线AB的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:x2+(y-a)2=4,点A(1,0).
(1)当过点A的圆C的切线存在时,求实数a的取值范围;
(2)设AM、AN为圆C的两条切线,M、N为切点,当MN=
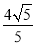 时,求MN所在直线的方程.
时,求MN所在直线的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,直线l:y=t(t≠0)交y轴于点M,交抛物线C:y2=2px(p>0)于点P,M关于点P的对称点为N,连结ON并延长交C于点H.
(1)求
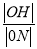 ;
;(2)除H以外,直线MH与C是否有其它公共点?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80 m.经测量,点A位于点O正北方向60 m处,点C位于点O正东方向170 m处(OC为河岸),tan∠BCO=
 .
.
(1)求新桥BC的长;
(2)当OM多长时,圆形保护区的面积最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆E:
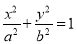 (a﹥b﹥0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点
(a﹥b﹥0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点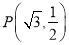 在椭圆E上.
在椭圆E上.(Ⅰ)求椭圆E的方程;
(Ⅱ)设不过原点O且斜率为
 的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:|MA|·|MB|=|MC|·|MD|.
的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:|MA|·|MB|=|MC|·|MD|.
相关试题

