搜索
【题目】如图所示，射线OA、OB分别与x轴正半轴成45°和30°角，过点P(1,0)作直线AB分别交OA、OB于A、B两点，当AB的中点C恰好落在直线y＝
x上时，求直线AB的方程．
参考答案：
【答案】(3＋
)x－2y－3－
＝0.
【解析】解：由题意可得kOA＝tan45°＝1，
kOB＝tan(180°－30°)＝－
，
所以射线OA的方程为y＝x(x≥0)，
射线OB的方程为y＝－
x(x≥0)．
设A(m，m)，B(－
n，n)，
所以AB的中点C(
， 
)，
由点C在y＝
x上，且A、P、B三点共线得
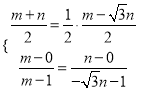
解得m＝
，
所以A(
， 
)．
又P(1,0)，
所以kAB＝kAP＝
＝
，
所以直线AB的方程为y＝
(x－1)，
即直线AB的方程为(3＋
)x－2y－3－
＝0.
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了净化空气，某科研单位根据实验得出，在一定范围内，每喷洒1个单位的净化剂，空气中释放的浓度y(单位：毫克/立方米)随着时间x(单位：天)变化的函数关系式近似为y＝
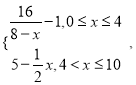若多次喷洒，则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和．由实验知，当空气中净化剂的浓度不低于4(毫克/立方米)时，它才能起到净化空气的作用．(1)若一次喷洒4个单位的净化剂，则净化时间可达几天？
(2)若第一次喷洒2个单位的净化剂，6天后再喷洒a(1≤a≤4)个单位的药剂，要使接下来的4天中能够持续有效净化，试求a的最小值(精确到0.1，参考数据:
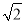取1.4)． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，已知两个正方形ABCD和DCEF不在同一平面内，M，N分别为AB，DF的中点．
(1)若平面ABCD⊥平面DCEF，求直线MN与平面DCEF所成角的正弦值；
(2)用反证法证明：直线ME与BN是两条异面直线．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f(x)的导函数f′(x)，且对任意x＞0，都有f′(x)＞
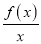.(1)判断函数F(x)＝
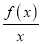在(0，＋∞)上的单调性；(2)设x1，x2∈(0，＋∞)，证明：f(x1)＋f(x2)＜f(x1＋x2)；
(3)请将(2)中结论推广到一般形式，并证明你所推广的结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知圆C：x2＋(y－a)2＝4，点A(1,0)．
(1)当过点A的圆C的切线存在时，求实数a的取值范围；
(2)设AM、AN为圆C的两条切线，M、N为切点，当MN＝
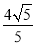时，求MN所在直线的方程． -
科目： 来源： 题型：
查看答案和解析>>【题目】在直角坐标系xOy中，曲线C1：
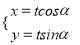(t为参数，t≠0)，其中0≤α＜π.在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ＝2sin θ，C3：ρ＝2
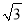cos θ.(1)求C2与C3交点的直角坐标；
(2)若C1与C2相交于点A，C1与C3相交于点B，求|AB|的最大值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在直角坐标系xOy中，直线l：y＝t(t≠0)交y轴于点M，交抛物线C：y2＝2px(p＞0)于点P，M关于点P的对称点为N，连结ON并延长交C于点H.
(1)求
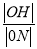；(2)除H以外，直线MH与C是否有其它公共点？说明理由．
相关试题
