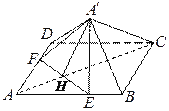
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,点
,点![]() 分别在边
分别在边![]() 上,
上, ![]() 与
与![]() 的交点为
的交点为![]() ,
, ![]() ,现将
,现将![]() 沿线段
沿线段![]() 折起到
折起到![]() 位置,使得
位置,使得![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求五棱锥![]() 的体积;
的体积;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() ;若不存在,说明理由.
;若不存在,说明理由.
参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)存在
;(3)存在![]() .
.
【解析】试题分析:(1)要证平面![]() 平面
平面![]() ,即证
,即证![]() 平面
平面![]() ;
;
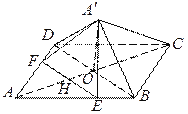
(2) 连接AC,设AC∩EF=H,由已知条件推导出平面A′HC⊥平面ABCD,过点A′作A′O垂直HC且与HC相交于点O,则A′O⊥平面ABCD,由此能求出五棱锥A′-BCDFE的体积.
(3)线段A′C上存在一点M,使得BM∥平面A′EF,A′M=.证明平面MBD∥平面A′EF, ![]() 即可得出结论.
即可得出结论.
试题解析:
(1)由![]() 是正方形,
是正方形, ![]() ,
, ![]() 是
是![]() 的中点,且
的中点,且![]() ,从而有
,从而有![]() 所以
所以![]() 平面
平面![]() , 从而平面,平面
, 从而平面,平面![]() .
.
(2)过点![]() 作
作![]() 垂直
垂直![]() 且与
且与![]() 相交于点
相交于点![]() ,由(1)知
,由(1)知![]() 平面
平面![]() ,
,
因为正方形![]() 的边长为
的边长为![]() ,
, ![]() ,得到:
,得到: ![]() ,
,
所以![]() ,所以
,所以![]()
所以五棱锥![]() 的体积
的体积![]() .
.
(3)线段![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,
, ![]() .
.
证明: ![]()
![]() ,
, ![]() ,所以
,所以![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() , 所以平面
, 所以平面![]() 平面
平面![]() ,
,
由![]() 在平面
在平面![]() 内,所以
内,所以![]() 平面
平面![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设双曲线
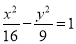 的左焦点为
的左焦点为 ,点
,点 为双曲线右支上的一点,且
为双曲线右支上的一点,且 与圆
与圆 相切于点
相切于点 为线段
为线段 的中点,
的中点,  为坐标原点,则
为坐标原点,则 __________.
__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】为对南康区和于都县两区县某次联考成绩进行分析,随机抽查了两地一共10000名考生的成绩,根据所得数据画了如下的样本频率分布直方图.

(1)求成绩在
 的频率;
的频率;(2)根据频率分布直方图算出样本数据平均数;
(3)为了分析成绩与班级、学校等方面的关系,必须按成绩再从这10000人中用分层抽样方法抽出20人作进一步分析,则成绩在
 的这段应抽多少人?
的这段应抽多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
 .
.(1)求曲线在点
 处的切线方程;
处的切线方程;(2)求过点
 的曲线的切线方程.
的曲线的切线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018江西南康中学、于都中学上学期第四次联考】椭圆
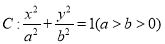 上动点
上动点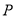 到两个焦点的距离之和为4,且到右焦点距离的最大值为
到两个焦点的距离之和为4,且到右焦点距离的最大值为 .
.(I)求椭圆
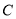 的方程;
的方程;(II)设点
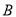 为椭圆的上顶点,若直线
为椭圆的上顶点,若直线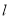 与椭圆
与椭圆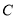 交于两点
交于两点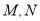 (
( 不是上下顶点)
不是上下顶点)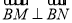 .试问:直线
.试问:直线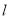 是否经过某一定点,若是,求出该定点的坐标;若不是,请说明理由;
是否经过某一定点,若是,求出该定点的坐标;若不是,请说明理由;(III)在(II)的条件下,求
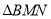 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一装有水的直三棱柱ABC-A1B1C1容器(厚度忽略不计),上下底面均为边长为5的正三角形,侧棱为10,侧面AA1B1B水平放置,如图所示,点D、E、F、G分别在棱CA、CB、C1B1、C1A1上,水面恰好过点D,E,F,C,且CD=2

(1)证明:DE∥AB;
(Ⅱ)若底面ABC水平放置时,求水面的高
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥A-BCDE中,底面BCDE为直角梯形,CD⊥平面ABC,侧面ABC是等腰直角三角形,∠EBC=∠ABC=90°,BC=CD=2BE=2,点M是棱AD的中点

(I)证明:平面AED⊥平面ACD;
(Ⅱ)求锐二面角B-CM-A的余弦值
相关试题

