【题目】已知曲线![]() .
.
(1)求曲线在点![]() 处的切线方程;
处的切线方程;
(2)求过点![]() 的曲线的切线方程.
的曲线的切线方程.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)根据曲线的解析式求出导函数,把P的横坐标代入导函数中即可求出切线的斜率,根据P的坐标和求出的斜率写出切线的方程即可;
(2)设出曲线过点P切线方程的切点坐标,把切点的横坐标代入到(1)求出的导函数中即可表示出切线的斜率,根据切点坐标和表示出的斜率,写出切线的方程,把P的坐标代入切线方程即可得到关于切点横坐标的方程,求出方程的解即可得到切点横坐标的值,分别代入所设的切线方程即可.
试题解析:
(1)![]()
![]() 在点
在点![]() 处的切线的斜率
处的切线的斜率![]()
![]() 曲线在点
曲线在点![]() 处的切线方程为
处的切线方程为![]() 即
即![]()
(2)设曲线![]() 与过点
与过点![]() 的切线相切于点
的切线相切于点![]() ,则切线的斜率
,则切线的斜率![]() ,
, ![]() 切线方程为
切线方程为![]() ,即
,即![]() .
.
![]() 点
点![]() 在切线上,
在切线上, ![]() ,即
,即![]() ,
,
![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,
,
故所求的切线方程为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,离心率
轴上,离心率 ,且椭圆
,且椭圆 经过点
经过点 ,过椭圆
,过椭圆 的左焦点
的左焦点 且不与坐标轴垂直的直线交椭圆
且不与坐标轴垂直的直线交椭圆 于
于 ,
,  两点.
两点.(1)求椭圆
 的方程;
的方程;(2)设线段
 的垂直平分线与
的垂直平分线与 轴交于点
轴交于点 ,求△
,求△ 的面积
的面积 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设双曲线
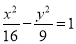 的左焦点为
的左焦点为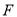 ,点
,点 为双曲线右支上的一点,且
为双曲线右支上的一点,且 与圆
与圆 相切于点
相切于点 为线段
为线段 的中点,
的中点,  为坐标原点,则
为坐标原点,则 __________.
__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】为对南康区和于都县两区县某次联考成绩进行分析,随机抽查了两地一共10000名考生的成绩,根据所得数据画了如下的样本频率分布直方图.

(1)求成绩在
 的频率;
的频率;(2)根据频率分布直方图算出样本数据平均数;
(3)为了分析成绩与班级、学校等方面的关系,必须按成绩再从这10000人中用分层抽样方法抽出20人作进一步分析,则成绩在
 的这段应抽多少人?
的这段应抽多少人? -
科目: 来源: 题型:
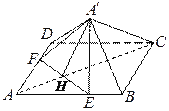
查看答案和解析>>【题目】如图,已知正方形
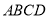 的边长为
的边长为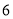 ,点
,点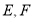 分别在边
分别在边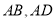 上,
上, 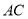 与
与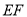 的交点为
的交点为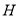 ,
, 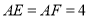 ,现将
,现将 沿线段
沿线段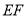 折起到
折起到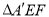 位置,使得
位置,使得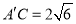 .
.
(1)求证:平面
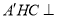 平面
平面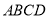 ;
;(2)求五棱锥
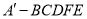 的体积;
的体积;(3)在线段
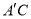 上是否存在一点
上是否存在一点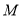 ,使得
,使得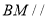 平面
平面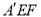 ?若存在,求
?若存在,求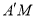 ;若不存在,说明理由.
;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018江西南康中学、于都中学上学期第四次联考】椭圆
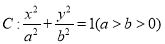 上动点
上动点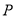 到两个焦点的距离之和为4,且到右焦点距离的最大值为
到两个焦点的距离之和为4,且到右焦点距离的最大值为 .
.(I)求椭圆
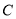 的方程;
的方程;(II)设点
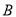 为椭圆的上顶点,若直线
为椭圆的上顶点,若直线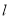 与椭圆
与椭圆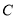 交于两点
交于两点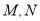 (
( 不是上下顶点)
不是上下顶点)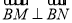 .试问:直线
.试问:直线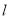 是否经过某一定点,若是,求出该定点的坐标;若不是,请说明理由;
是否经过某一定点,若是,求出该定点的坐标;若不是,请说明理由;(III)在(II)的条件下,求
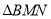 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一装有水的直三棱柱ABC-A1B1C1容器(厚度忽略不计),上下底面均为边长为5的正三角形,侧棱为10,侧面AA1B1B水平放置,如图所示,点D、E、F、G分别在棱CA、CB、C1B1、C1A1上,水面恰好过点D,E,F,C,且CD=2

(1)证明:DE∥AB;
(Ⅱ)若底面ABC水平放置时,求水面的高
相关试题

