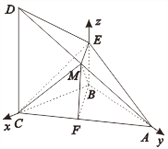
【题目】已知四棱锥A-BCDE中,底面BCDE为直角梯形,CD⊥平面ABC,侧面ABC是等腰直角三角形,∠EBC=∠ABC=90°,BC=CD=2BE=2,点M是棱AD的中点

(I)证明:平面AED⊥平面ACD;
(Ⅱ)求锐二面角B-CM-A的余弦值
参考答案:
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(1)![]() 平面ACD,又EM//BF,所以
平面ACD,又EM//BF,所以![]() 平面ACD,所以平面
平面ACD,所以平面![]() 平面
平面![]() ;(2)建立空间直角坐标系,求得两个法向量
;(2)建立空间直角坐标系,求得两个法向量![]() ,
,![]() ,求出二面角。
,求出二面角。
试题解析:
(I)证明:取AC的中点F,连接BF,
因为AB=BC,所以![]() ,
, ![]() 平面ABC,所以CD
平面ABC,所以CD ![]() .
.
又![]() 所以
所以![]() 平面ACD.①
平面ACD.①
因为AM=MD,AF=CF,所以![]() .
.
因为![]()
![]() ,所以
,所以![]() //MF,
//MF,
所以四边形BFME是平行四边形.所以EM//BF.②
由①②,得![]() 平面ACD,所以平面
平面ACD,所以平面![]() 平面
平面![]() ;
;
(II)![]() BE
BE![]() 平面ABC,
平面ABC,
![]() 又
又![]() ,
,
![]() 以点B为原点,直线BC、BA、BE分别为x,y,z轴,
以点B为原点,直线BC、BA、BE分别为x,y,z轴,
建立空间直角坐标系B-xyz.
由![]() ,得B(0,0,0),C(2,0,0),A(0,2,0),D(2,0,2).
,得B(0,0,0),C(2,0,0),A(0,2,0),D(2,0,2).
由中点坐标公式得![]() ,
, ![]() ,
,![]() ,
,
设向量![]() 为平面BMC的一个法向量,则
为平面BMC的一个法向量,则![]() 即
即![]()
令y=1,得x=0,z=-1,即![]() ,
,
由(I)知, ![]() 是平面ACD的一个法向量.
是平面ACD的一个法向量.
设二面角B-CM-A的平面角为![]() ,
,
则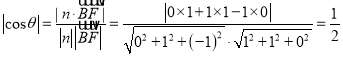 ,
,
又二面角B-CM-A为锐二面角,故![]() .
.
-
科目: 来源: 题型:
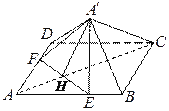
查看答案和解析>>【题目】如图,已知正方形
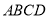 的边长为
的边长为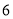 ,点
,点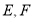 分别在边
分别在边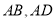 上,
上, 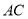 与
与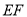 的交点为
的交点为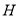 ,
, 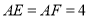 ,现将
,现将 沿线段
沿线段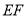 折起到
折起到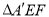 位置,使得
位置,使得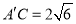 .
.
(1)求证:平面
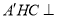 平面
平面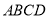 ;
;(2)求五棱锥
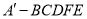 的体积;
的体积;(3)在线段
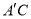 上是否存在一点
上是否存在一点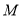 ,使得
,使得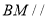 平面
平面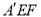 ?若存在,求
?若存在,求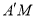 ;若不存在,说明理由.
;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018江西南康中学、于都中学上学期第四次联考】椭圆
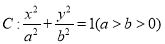 上动点
上动点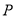 到两个焦点的距离之和为4,且到右焦点距离的最大值为
到两个焦点的距离之和为4,且到右焦点距离的最大值为 .
.(I)求椭圆
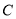 的方程;
的方程;(II)设点
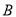 为椭圆的上顶点,若直线
为椭圆的上顶点,若直线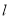 与椭圆
与椭圆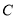 交于两点
交于两点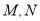 (
( 不是上下顶点)
不是上下顶点)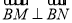 .试问:直线
.试问:直线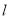 是否经过某一定点,若是,求出该定点的坐标;若不是,请说明理由;
是否经过某一定点,若是,求出该定点的坐标;若不是,请说明理由;(III)在(II)的条件下,求
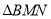 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一装有水的直三棱柱ABC-A1B1C1容器(厚度忽略不计),上下底面均为边长为5的正三角形,侧棱为10,侧面AA1B1B水平放置,如图所示,点D、E、F、G分别在棱CA、CB、C1B1、C1A1上,水面恰好过点D,E,F,C,且CD=2

(1)证明:DE∥AB;
(Ⅱ)若底面ABC水平放置时,求水面的高
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙H被直线x-y-1=0,x+y-3=0分成面积相等的四个部分,且截x轴所得线段的长为2。
(I)求⊙H的方程;
(Ⅱ)若存在过点P(0,b)的直线与⊙H相交于M,N两点,且点M恰好是线段PN的中点,求实数b的取值范围
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
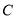 :
: 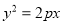 的焦点为
的焦点为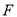 ,准线为
,准线为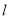 ,三个点
,三个点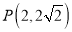 ,
, 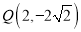 ,
, 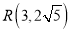 中恰有两个点在
中恰有两个点在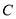 上.
上.(1)求抛物线
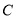 的标准方程;
的标准方程;(2)过
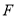 的直线交
的直线交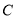 于
于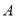 ,
, 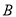 两点,点
两点,点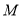 为
为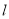 上任意一点,证明:直线
上任意一点,证明:直线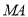 ,
, 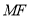 ,
, 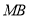 的斜率成等差数列.
的斜率成等差数列. -
科目: 来源: 题型:
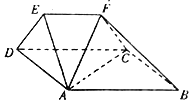
查看答案和解析>>【题目】如图在多面体
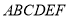 中,四边形
中,四边形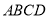 是边长为
是边长为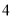 的正方形,
的正方形, 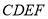 为等腰梯形,且
为等腰梯形,且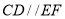 ,
, 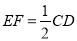 ,
, 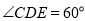 ,
, 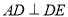 .
.
(1)证明:平面
 平面
平面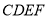 ;
;(2)求二面角
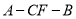 的余弦值.
的余弦值.
相关试题

