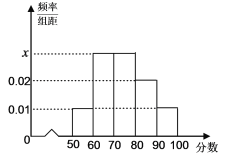
【题目】2018年高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试,现从这些学生中随机抽取了50名学生的成绩,按照成绩为![]() ,
,![]() ,…,
,…,![]() 分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
(Ⅰ)求频率分布直方图中的![]() 的值,并估计所抽取的50名学生成绩的中位数(用分数表示);
的值,并估计所抽取的50名学生成绩的中位数(用分数表示);
(Ⅱ)若利用分层抽样的方法从样本中成绩不低于70分的三组学生中抽取6人,再从这6人中随机抽取2人参加这次考试的考后分析会,试求![]() 组中至少有1人被抽到的概率.
组中至少有1人被抽到的概率.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】分析:(Ⅰ)先计算第2、3组的频率和,再根据概率求x的值,再利用中位数公式求所抽取的50名学生成绩的中位数.( Ⅱ)利用古典概型求![]() 组中至少有1人被抽到的概率.
组中至少有1人被抽到的概率.
详解:(Ⅰ)由频率分布直方图可得第2、3组的频率和为
![]() , 故
, 故![]() .
.
设中位数为![]() 分,则有
分,则有![]() ,
,![]() ,
,
即所求的中位数为![]() 分.
分.
(Ⅱ)由(Ⅰ)可知,后三组中的人数分别为15,10,5,故这三组中所抽取的人数分别为3,2,1.
记成绩在![]() 这组的3名学生分别为
这组的3名学生分别为![]() ,
,![]() ,
,![]() ,成绩在
,成绩在![]() 这组的2名学生分别为
这组的2名学生分别为![]() ,
,![]() ,成绩在
,成绩在![]() 这组的1名学生为
这组的1名学生为![]() ,则从中任抽取3人的所有可能结果为
,则从中任抽取3人的所有可能结果为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .共15种.
.共15种.
其中![]() 组中至少有1人被抽到的所有可能结果为
组中至少有1人被抽到的所有可能结果为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .共12种
.共12种
故![]() 组中至少有1人被抽到的概率
组中至少有1人被抽到的概率![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),等腰直角三角形
 的底边
的底边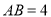 ,点
,点 在线段
在线段 上,
上, 于
于 ,现将
,现将 沿
沿 折起到
折起到 的位置(如图(2))
的位置(如图(2))
(1)求证:
 ;
;(2)若
 ,直线
,直线 与平面
与平面 所成的角为
所成的角为 ,求
,求 长.
长. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校高三毕业生报考体育专业学生的体重(单位:千克)情况,将他们的体重数据整理后得到如下频率分布直方图,已知图中从左至右前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
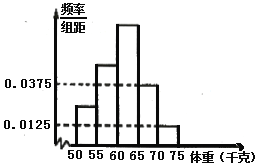
(Ⅰ)求该校报考体育专业学生的总人数
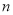 ;
;(Ⅱ)已知A,
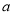 是该校报考体育专业的两名学生,A的体重小于55千克,
是该校报考体育专业的两名学生,A的体重小于55千克,  的体重不小于70千克,现从该校报考体育专业的学生中按分层抽样分别抽取体重小于55千克和不小于70千克的学生共6名,然后再从这6人中抽取体重小于55千克学生1人,体重不小于70千克的学生2人组成3人训练组,求A不在训练组且
的体重不小于70千克,现从该校报考体育专业的学生中按分层抽样分别抽取体重小于55千克和不小于70千克的学生共6名,然后再从这6人中抽取体重小于55千克学生1人,体重不小于70千克的学生2人组成3人训练组,求A不在训练组且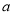 在训练组的概率.
在训练组的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,动点
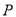 到两点
到两点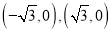 的距离之和等于4,设点
的距离之和等于4,设点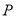 的轨迹为曲线
的轨迹为曲线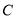 ,直线
,直线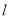 过点
过点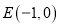 且与曲线
且与曲线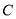 交于
交于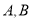 两点.
两点.(Ⅰ)求曲线
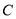 的方程;
的方程;(Ⅱ)
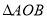 的面积是否存在最大值,若存在,求出
的面积是否存在最大值,若存在,求出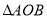 的面积的最大值;若不存在,说明理由.
的面积的最大值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
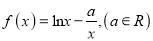 .
.(Ⅰ)判断
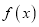 的单调性;
的单调性;(Ⅱ)若
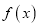 在
在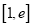 上的最小值为2,求
上的最小值为2,求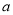 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】“
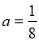 ”是“对任意的正数
”是“对任意的正数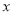 ,
, 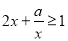 ”的( )
”的( )A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
【答案】A
【解析】分析:根据基本不等式,我们可以判断出“
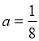 ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+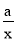 ≥1”与“对任意的正数x,2x+
≥1”与“对任意的正数x,2x+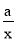 ≥1”?“a=
≥1”?“a=”真假,进而根据充要条件的定义,即可得到结论.
解答:解:当“a=
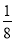 ”时,由基本不等式可得:
”时,由基本不等式可得:“对任意的正数x,2x+
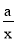 ≥1”一定成立,
≥1”一定成立,即“a=
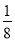 ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+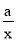 ≥1”为真命题;
≥1”为真命题;而“对任意的正数x,2x+
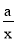 ≥1的”时,可得“a≥
≥1的”时,可得“a≥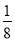 ”
”即“对任意的正数x,2x+
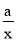 ≥1”?“a=
≥1”?“a=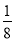 ”为假命题;
”为假命题;故“a=
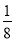 ”是“对任意的正数x,2x+
”是“对任意的正数x,2x+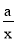 ≥1的”充分不必要条件
≥1的”充分不必要条件故选A
【题型】单选题
【结束】
9【题目】如图是一几何体的平面展开图,其中
 为正方形,
为正方形,  ,
,  分别为
分别为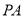 ,
, 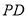 的中点,在此几何体中,给出下面四个结论:①直线
的中点,在此几何体中,给出下面四个结论:①直线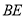 与直线
与直线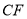 异面;②直线
异面;②直线 与直线
与直线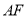 异面;③直线
异面;③直线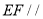 平面
平面 ;④平面
;④平面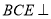 平面
平面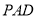 .
.其中一定正确的选项是( )

A. ①③ B. ②③ C. ②③④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣a|+|x+5﹣a|
(1)若不等式f(x)﹣|x﹣a|≤2的解集为[﹣5,﹣1],求实数a的值;
(2)若x0∈R,使得f(x0)<4m+m2 , 求实数m的取值范围.
相关试题

