【题目】关于函数f(x)=sin(x﹣![]() )sin(x+
)sin(x+![]() ),有下列命题:
),有下列命题:
①此函数可以化为f(x)=﹣![]() sin(2x+
sin(2x+![]() );
);
②函数f(x)的最小正周期是π,其图象的一个对称中心是(![]() , 0);
, 0);
③函数f(x)的最小值为﹣![]() , 其图象的一条对称轴是x=
, 其图象的一条对称轴是x=![]() ;
;
④函数f(x)的图象向右平移![]() 个单位后得到的函数是偶函数;
个单位后得到的函数是偶函数;
⑤函数f(x)在区间(﹣![]() , 0)上是减函数.
, 0)上是减函数.
其中所有正确的命题的序号个数是( )
A.2
B.3
C.4
D.5
参考答案:
【答案】C
【解析】①f(x)=sin(x﹣![]() )sin(x+
)sin(x+![]() )=﹣
)=﹣![]() [cos(2x+
[cos(2x+![]() )﹣cos(﹣
)﹣cos(﹣![]() )]=﹣
)]=﹣![]() cos(2x+
cos(2x+![]() )=﹣
)=﹣![]() sin[
sin[![]() ﹣(2x+
﹣(2x+![]() )]=﹣
)]=﹣![]() sin(
sin(![]() ﹣2x)=﹣
﹣2x)=﹣![]() sin[π﹣(
sin[π﹣(![]() ﹣2x)]=﹣
﹣2x)]=﹣![]() sin(2x+
sin(2x+![]() ),故正确;
),故正确;
②由①得f(x)=﹣![]() cos(2x+
cos(2x+![]() ),从而解得T=
),从而解得T=![]() =π,令2x+
=π,令2x+![]() =k
=k![]() +
+![]() 可解得:x=
可解得:x=![]() +
+![]() , k∈Z,故k=0时,(
, k∈Z,故k=0时,(![]() , 0)是一个对称中心.故正确;
, 0)是一个对称中心.故正确;
③由①得f(x)=﹣![]() cos(2x+
cos(2x+![]() ),令2x+
),令2x+![]() =kπ可解得:x=
=kπ可解得:x=![]() -
-![]() k∈Z,故k=1时,图象的一条对称轴是x=
k∈Z,故k=1时,图象的一条对称轴是x=![]() , 函数f(x)的最小值为﹣
, 函数f(x)的最小值为﹣![]() . 故正确;
. 故正确;
④函数f(x)的图象向右平移![]() 个单位后得到的函数为f(x﹣
个单位后得到的函数为f(x﹣![]() )=﹣
)=﹣![]() cos[2(x﹣
cos[2(x﹣![]() )+
)+![]() ]=﹣
]=﹣![]() cos[2x﹣
cos[2x﹣![]() +
+![]() ]=﹣
]=﹣![]() cos2x,是偶函数,故正确;
cos2x,是偶函数,故正确;
⑤由①得f(x)=﹣![]() cos(2x+
cos(2x+![]() ),令2kπ﹣π≤2x+
),令2kπ﹣π≤2x+![]() ≤2π,可解得:
≤2π,可解得:![]() -
-![]() ≤x≤k
≤x≤k![]() -
-![]() , k∈Z,即当k=0时函数f(x)在区间(﹣
, k∈Z,即当k=0时函数f(x)在区间(﹣![]() , ﹣
, ﹣![]() )上是减函数,故不正确.
)上是减函数,故不正确.
综上可得,所有正确的命题的序号个数是4个.
故选:C.
【考点精析】解答此题的关键在于理解三角函数的积化和差公式的相关知识,掌握三角函数的积化和差公式:![]() ;
;![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,江的两岸可近似的看成两平行的直线,江岸的一侧有A,B两个蔬菜基地,江的另一侧点C处有一个超市.已知A、B、C中任意两点间的距离为20千米.超市欲在AB之间建一个运输中转站D,A,B两处的蔬菜运抵D处后,再统一经过货轮运抵C处.由于A,B两处蔬菜的差异,这两处的运输费用也不同.如果从A处出发的运输费为每千米2元,从B处出发的运输费为每千米1元,货轮的运输费为每千米3元.

(1)设∠ADC=α,试将运输总费用S(单位:元)表示为α的函数S(α),并写出自变量的取值范围;
(2)问中转站D建在何处时,运输总费用S最小?并求出最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,平面
中,平面 平面
平面 ;
;  ,
,  ,
,  ,
,  .
.(1)证明:
 平面
平面 ;
;(2)求直线
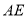 与平面
与平面 所成的角的正切值.
所成的角的正切值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD与BDEF均为菱形,设AC与BD相交于点O,若∠DAB=∠DBF=60°,且FA=FC.
(1)求证:FC∥平面EAD;
(2)求二面角A-FC-B的余弦值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列4个函数:①
 ;②y=sinx;③y=﹣tanx;④y=﹣cos2x、其中在区间
;②y=sinx;③y=﹣tanx;④y=﹣cos2x、其中在区间  上增函数且以π为周期的函数是(把所有符合条件的函数序列号都填上)
上增函数且以π为周期的函数是(把所有符合条件的函数序列号都填上) -
科目: 来源: 题型:
查看答案和解析>>【题目】某地一天中6时至14时的温度变化曲线近似满足函数T=Asin(ωt+φ)+B(其中
 <φ<π)6时至14时期间的温度变化曲线如图所示,它是上述函数的半个周期的图象,那么图中曲线对应的函数解析式是 .
<φ<π)6时至14时期间的温度变化曲线如图所示,它是上述函数的半个周期的图象,那么图中曲线对应的函数解析式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(-1,0),B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是________
相关试题

