【题目】在下列4个函数:① ![]() ;②y=sinx;③y=﹣tanx;④y=﹣cos2x、其中在区间
;②y=sinx;③y=﹣tanx;④y=﹣cos2x、其中在区间 ![]() 上增函数且以π为周期的函数是(把所有符合条件的函数序列号都填上)
上增函数且以π为周期的函数是(把所有符合条件的函数序列号都填上)
参考答案:
【答案】④
【解析】y=sin ![]() 的最小正周期T=
的最小正周期T= 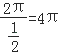 ,不符合要求;
,不符合要求;
y=sinx的最小正周期T=2π,不符合题意;
y=﹣tanx的最小正周期T=π但是在 ![]() 上单调递减,不符合题意;
上单调递减,不符合题意;
y=﹣cos2x的最小正周期T= ![]() ,令2kπ≤2x≤π+2kπ,∴kπ≤x≤
,令2kπ≤2x≤π+2kπ,∴kπ≤x≤ ![]()
∴y=﹣cos2x在[kπ, ![]() ]上单调递增,故在区间
]上单调递增,故在区间 ![]() 上增,满足条件.
上增,满足条件.
所以答案是:④
【考点精析】关于本题考查的正弦函数的单调性和正切函数的单调性,需要了解正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数;正切函数的单调性:在
上是减函数;正切函数的单调性:在![]() ;
;![]() 上是增函数才能得出正确答案.
上是增函数才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<
 )的最高点D的坐标(
)的最高点D的坐标(  ,2),由D点运动到相邻最低点时函数曲线与x轴的交点(
,2),由D点运动到相邻最低点时函数曲线与x轴的交点( 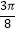 ,0)
,0)
(1)求f(x)的解析式
(2)求f(x)的单调增区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax3+bx2+cx在x=±1处取得极值,且在x=0处的切线的斜率为﹣3.
(1)求f(x)的解析式;
(2)求过点A(2,2)的切线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
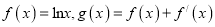 .
.(I)求
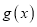 的单调区间和最小值;
的单调区间和最小值;(II)讨论
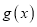 与
与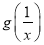 的大小关系;
的大小关系;(III)求
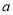 的取值范围,使得
的取值范围,使得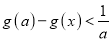 对任意
对任意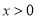 恒成立.
恒成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件。已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,PA⊥底面ABCD,AB⊥AC,AB=1,BC=2,PA=
 ,E为BC的中点.
,E为BC的中点. 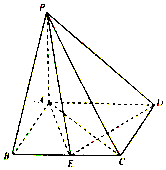
(1)证明:PE⊥ED;
(2)求二面角E﹣PD﹣A的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn , 且Sn=2an﹣2,数列{bn}满足b1=1,且bn+1=bn+2.
(1)求数列{an},{bn}的通项公式;
(2)设cn=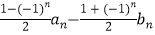 ,求数列{cn}的前2n项和T2n .
,求数列{cn}的前2n项和T2n .
相关试题

