【题目】若点P是直线2x+y+10=0上的动点,直线PA、PB分别与圆x2+y2=4相切于A、B两点,则四边形PAOB(O为坐标原点)面积的最小值为________.
参考答案:
【答案】8
【解析】
由题意可得,PA=PB,PA⊥OA,PB⊥OB则要求SPAOB=2S△PAO=![]() 的最小值,转化为求PA最小值,由于PA2=PO2﹣4,当PO最小时,PA最小,结合点到直线的距离公式可知当PO⊥l时,PO有最小值,由点到直线的距离公式可求
的最小值,转化为求PA最小值,由于PA2=PO2﹣4,当PO最小时,PA最小,结合点到直线的距离公式可知当PO⊥l时,PO有最小值,由点到直线的距离公式可求
:由题意可得,PA=PB,PA⊥OA,PB⊥OB
SPAOB=2S△PAO=![]()
又∵在Rt△PAO中,由勾股定理可得,PA2=PO2﹣4,当PO最小时,PA最小,此时所求的面积也最小
点P是直线l:2x+y+10=0上的动点,
当PO⊥l时,PO有最小值d=![]() ,PA=4
,PA=4
所求四边形PAOB的面积的最小值为8
故答案为:8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四面体
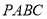 中,
中, 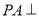 平面
平面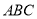 ,
, 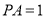 ,
, 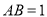 ,
,  ,
,  .
.(Ⅰ)求四面体
 的四个面的面积中,最大的面积是多少?
的四个面的面积中,最大的面积是多少?(Ⅱ)证明:在线段
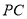 上存在点
上存在点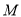 ,使得
,使得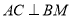 ,并求
,并求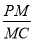 的值.
的值.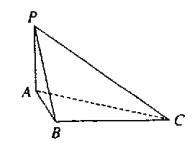
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直线l:3x-y-1=0上求点P和Q,使得
(1)点P到点A(4,1)和B(0,4)的距离之差最大;
(2)点Q到点A(4,1)和C(3,4)的距离之和最小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】动圆M与定圆C:x2+y2+4x=0相外切,且与直线l:x-2=0相切,则动圆M的圆心的轨迹方程为( )
A. y2-12x+12=0 B. y2+12x-12=0
C. y2+8x=0 D. y2-8x=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】若圆x2+y2-4x-4y-10=0上至少有三个不同点到直线l:ax+by=0的距离为2
 ,求直线l斜率的取值范围.
,求直线l斜率的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数x,y满足方程x2+y2-4x+1=0.
(1)求
 的最大值和最小值;
的最大值和最小值;(2)求y-x的最大值和最小值;
(3)求x2+y2的最大值和最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线l过点(1,0)且被两条平行直线l1:3x+y-6=0和l2:3x+y+3=0所截得的线段长为
 ,求直线l的方程.
,求直线l的方程.
相关试题

