【题目】某地区2008年至2014年中,每年的居民人均纯收入y(单位:千元)的数据如下表:
年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
对变量t与y进行相关性检验,得知t与y之间具有线性相关关系.
(1)求y关于t的线性回归方程;
(2)预测该地区2017年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
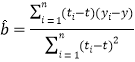 ,
,![]()
参考答案:
【答案】(1)![]() (2)预测该地区2017年的居民人均收入为
(2)预测该地区2017年的居民人均收入为![]() 千元
千元
【解析】试题分析:(1)由公式分别算出![]() ,
,![]() ,
,![]() ,
,![]() ,进一步算出
,进一步算出![]() ,
,![]() ,即求出线性回归方程。(2)2017年的年份代号
,即求出线性回归方程。(2)2017年的年份代号![]() 代入前面的回归方程求出
代入前面的回归方程求出![]() 、
、
试题解析:(1)由已知表格的数据,得![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
∴![]() .
.
∴![]() .
.
∴y关于t的线性回归方程是![]() .
.
(2)由(1),知y关于t的线性回归方程是![]() .
.
将2017年的年份代号![]() 代入前面的回归方程,得
代入前面的回归方程,得![]() .
.
故预测该地区2017年的居民人均收入为![]() 千元.
千元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
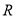 上的函数
上的函数 的图像经过点
的图像经过点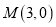 ,且
,且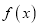 在区间
在区间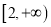 单调递减,又知函数
单调递减,又知函数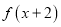 为偶函数,则关于
为偶函数,则关于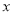 的不等式
的不等式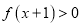 的解为 ( )
的解为 ( )A.
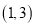 B.
B. 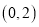 C.
C. 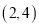 D.
D. 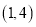
-
科目: 来源: 题型:
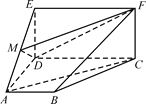
查看答案和解析>>【题目】如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,
 ,M是线段AE上的动点.
,M是线段AE上的动点.(1)试确定点M的位置,使AC∥平面DMF,并说明理由;
(2)在(1)的条件下,求平面DMF与平面ABCD所成锐二面角的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
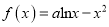 .
.(1)当
 时,求函数
时,求函数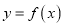 在
在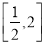 上的最大值;
上的最大值;(2)令
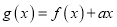 ,若
,若 在区间
在区间 上为单调递增函数,求
上为单调递增函数,求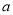 的取值范围;
的取值范围;(3)当
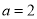 时,函数
时,函数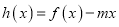 的图象与
的图象与 轴交于两点
轴交于两点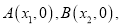 且
且 ,又
,又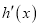 是
是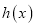 的导函数.若正常数
的导函数.若正常数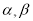 满足条件
满足条件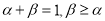 .证明:
.证明: 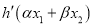 <0.
<0. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
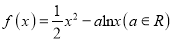 .
.(I)若函数
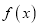 在
在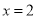 处的切线方程为
处的切线方程为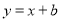 ,求
,求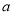 和
和 的值;
的值;(II)讨论方程
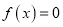 的解的个数,并说明理由.
的解的个数,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
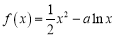 .
.(Ⅰ)若函数
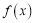 的图像在
的图像在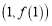 处的切线不过第四象限且不过原点,求
处的切线不过第四象限且不过原点,求 的取值范围;
的取值范围;(Ⅱ)设
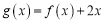 ,若
,若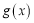 在
在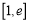 上不单调且仅在
上不单调且仅在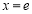 处取得最大值,求
处取得最大值,求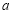 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)为定义在R上的奇函数.如图是函数图象的一部分,当0≤x≤2时,是线段OA;当x>2时,图象是顶点为P(3,4)的抛物线的一部分.
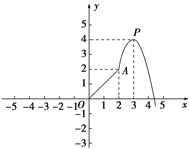
(1)在图中的直角坐标系中画出函数f(x)的图象;
(2)求函数f(x)在[2,+∞)上的解析式;
(3)写出函数f(x)的单调区间.
相关试题

